






| 1 |
| 2 |
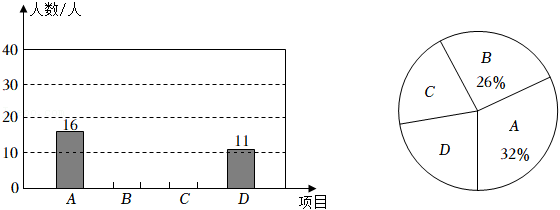
| 第一周做家务的时间(小时) | 0 | 1 | 2 | 3 | 4 |
| 人数(人) | 2 | 4 | 18 | 16 | 10 |
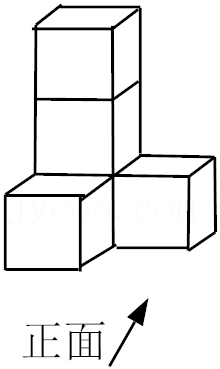
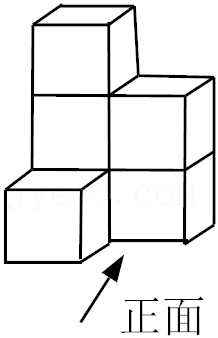
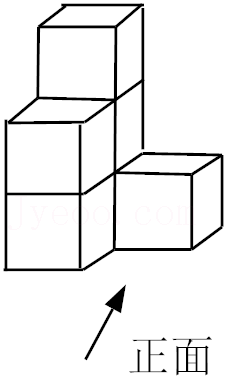
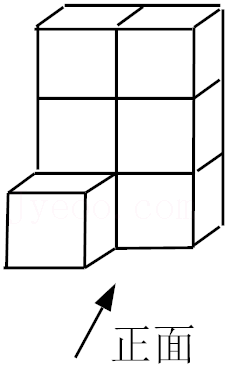
| 1 |
| 2 |
| 1 |
| 3 |
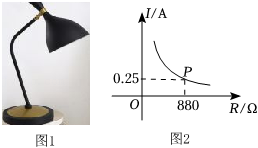
| 200 |
| R |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| x |
| k |
| x |
| k |
| x |
| 9 |
| 10 |
| 品名 | 甲种保健醋 | 乙种保健醋 |
| 售价(元) | 8.0 | 6.5 |
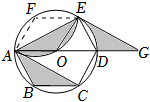
阿基米德(公元前287年-公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家、静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,留给后人的最有价值的书是《阿基米德全集》.在该书的“引理集”中有这样一道题:如图1,以AB为直径作半圆O,弦AC是一个内接正五边形的一条边(即:∠AOC=72°),点D是⌒AC的中点,连接CD并延长与直径BA的延长线交于点E,连接AC,DB交于点F,过点F作FM⊥AB于点M.求证:ME是半圆的半径.下面是勤奋小组的部分证明过程:证明:如图2,过点D作DH⊥AB于点H.∵∠AOC=72°,⌒AC=⌒AC∴∠ABC=
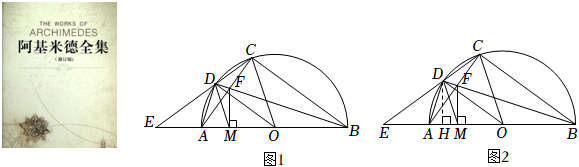 |
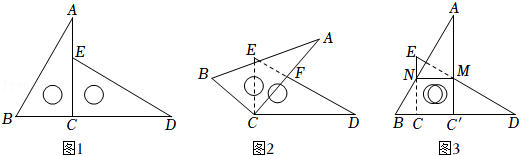
| 1 |
| 4 |
| 1 |
| 4 |