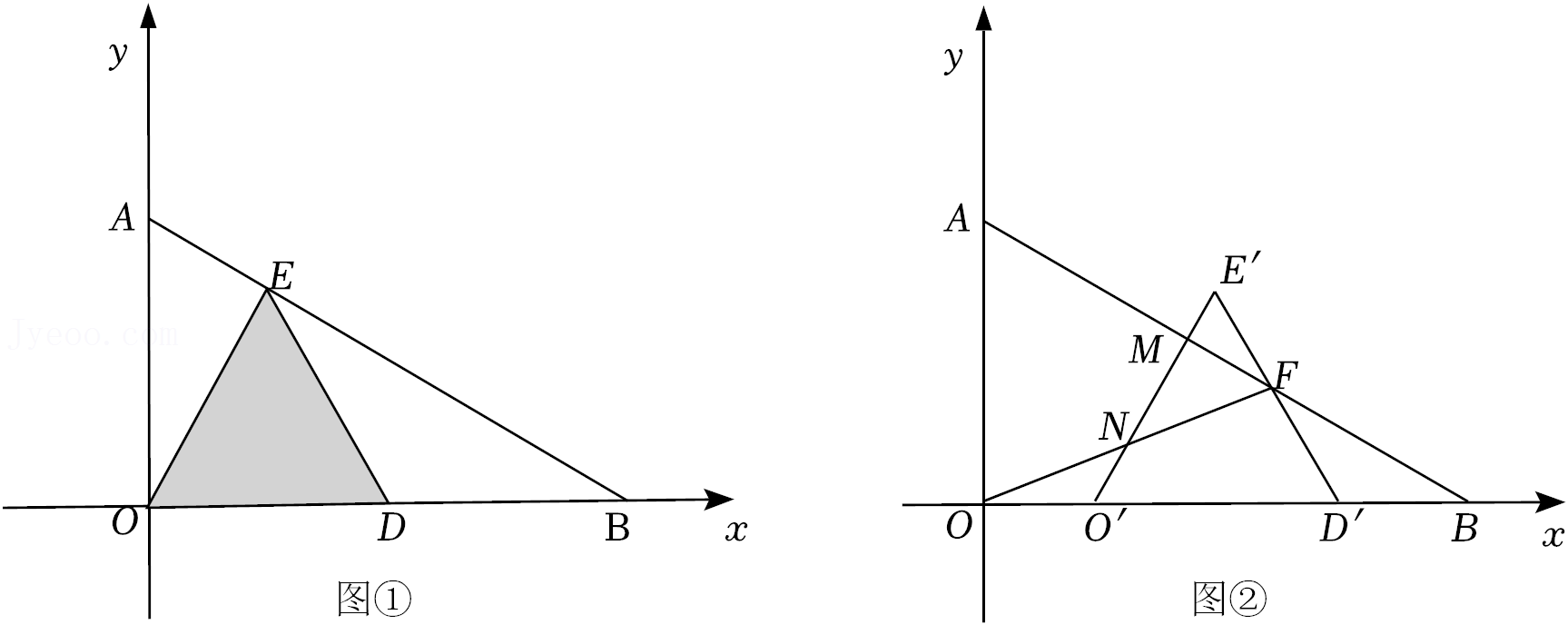
24.在平面直角坐标系中,O为原点,△OAB是直角三角形,∠AOB=90°,OA=
,OB=4,点A在y轴正半轴,点B在x轴正半轴,D点从O点出发,沿x轴正半轴方向运动,以OD为边在第一象限内作等边△ODE.
(1)如图①,当E恰好落在线段AB上,求OE的长;
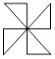
(2)在(1)的条件下,把△OED沿x轴正方向平移得到△O′E′D',点O,D,E的对应点分别为O′,D′,E′,线段D′E′和O'E′与线段AB分别交于点F和点M,连接OF交O'E′于点N.在平移过程中,
①设OO'的长为x,△O′D'E′与△AOB重叠部分的面积为y,试用含有x的代数式表示y,并直接写出x的取值范围;
②线段MN的长为
;
(3)点D在运动过程中,设OD的长为t,△ODE与△AOB重叠部分的面积为S,当S最大时,点D停止运动,将△AOB绕点O顺时针旋转得到△A'OB',点A,B的对应点分别为A′,B',连接EA′,EB′,直接写出△EA'B'面积的取值范围.