


| 1 |
| 3 |
| 1 |
| 3 |




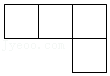


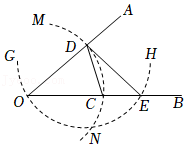
| 1 |
| 1-a |
| 1 |
| 1-3 |
| 1 |
| 2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
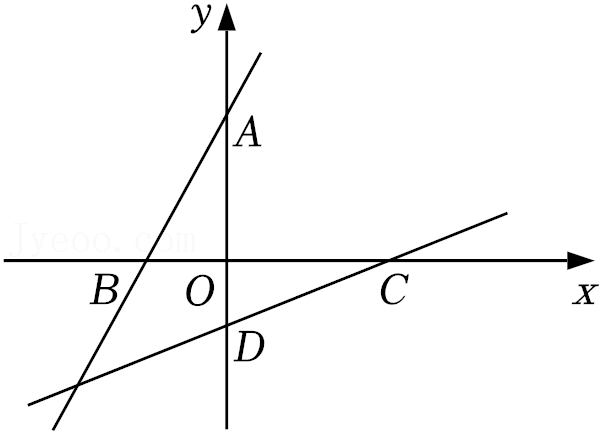
| 1 |
| 3 |
| 1 |
| 3 |
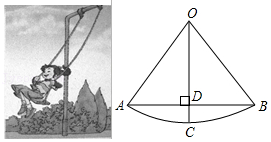
| 1 |
| 3 |
| 1 |
| m |
| 1 |
| n |
| k |
| x |
| 1 |
| a+1 |
| a |
| a2-1 |
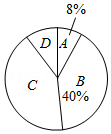
| 等级 | 成绩n/分 | 频数 |
| A | 94.5<n≤100 | 2 |
| 89.5<n<94.5 | ||
| B | 84.5<n<89.5 | 6 |
| 79.5<n<84.5 | 14 | |
| C | 74.5<n<79.5 | 16 |
| 69.5<n<74.5 | ||
| D | 64.5<n<69.5 | 3 |
| 59.5<n<64.5 | 2 |
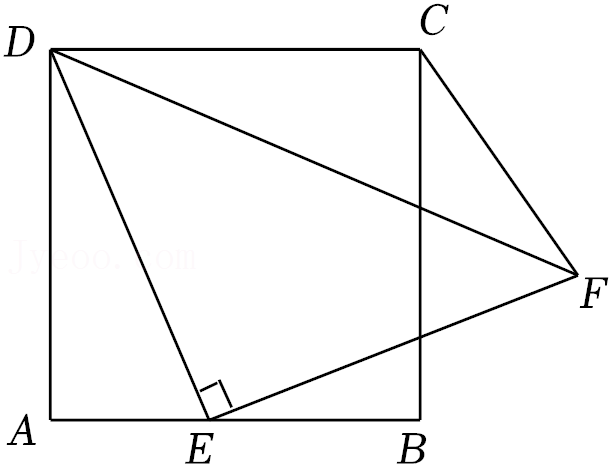
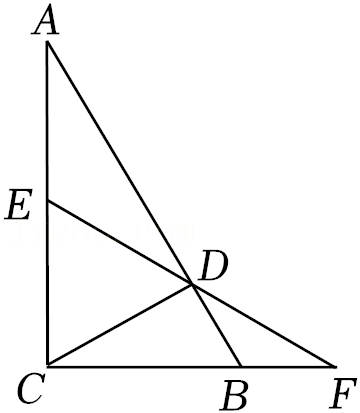
| FD |
| FC |
| 1 |
| 2 |
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| z2 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 52 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (-5)2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| (-5) |
| 19 |
| 30 |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 20192 |
| 1 |
| 20202 |
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| z2 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |