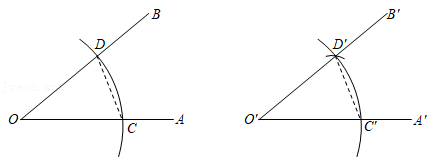17．计算：|-2|-()^-1+(π-3.14)⁰+cos45°．

18．先化简，再求值：3(a²b-2ab²-1)-2(2a²b-3ab²)+1，其中a=2，b=-1．

19．人教版初中数学教科书八年级上册第36、37页告诉我们作一个角等于已知角的方法：
已知：∠AOB．
求作：∠A′O′B′，使∠A′O′B′=∠AOB．
作图：(1)以O为圆心，任意长为半径画弧，分别交OA、OB于点C、D；
(2)画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
(3)以点C′为圆心，CD长为半径画弧，与第2步中所画的弧相交于点D′；
(4)过点D′画射线O′B′，则∠A′O′B′=∠AOB．

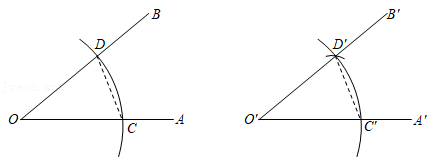
请你根据以上材料完成下列问题：
(1)完成下面证明过程(将正确答案写在相应的横线上)．
证明：由作图可知，在△O′C′D′和△OCD中，
，
∴△O′C′D′≌      ，
∴∠A′O′B'=∠AOB．
(2)这种作一个角等于已知角的方法依据是       ．(填序号)
①AAS；②ASA；③SSS；④SAS．

20．某学校想了解学生家长对“双减”政策的认知情况，随机抽查了部分学生家长进行调查，将抽查的数据结果进行统计，并绘制两幅不完整的统计图(A：不太了解，B：基本了解，C：比较了解，D：非常了解)．请你根据图中提供的信息回答以下问题：

(1)请求出这次被调查的学生家长共有多少人？
(2)请补全条形统计图．
(3)试求出扇形统计图中“比较了解”部分所对应的圆心角度数．
(4)该学校共有1200名学生家长，估计对“双减”政策了解程度为“非常了解”的学生家长大约有多少？

21．如图，在⊙O中，AB、AC是互相垂直且相等的两条弦，OD⊥AB，OE⊥AC，垂足分别为D、E．
(1)求证：四边形ADOE是正方形；
(2)若AC=2cm，求⊙O的半径．

22．为推进垃圾分类，推动绿色发展，某工厂购进甲、乙两种型号的机器人用来进行垃圾分类，甲种机器人比乙种机器人每小时多分20kg，甲种机器人分类900kg垃圾所用的时间与乙种机器人分类700kg垃圾所用的时间相等．
(1)甲乙两种机器人每小时各分类多少垃圾？
(2)现在两种机器人共同分类860kg垃圾，工作2小时后乙种机器人因机器维修退出，求乙种机器人退出后甲种机器人还需工作多长时间才能完成？

23．如图，△ABC中，∠ACB=90°，CD⊥AB于点D，∠ACD=3∠BCD，E是斜边AB的中点．
(1)证明：CD=DE；
(2)若AB=4，求BD的长；
(3)若BD=-1，求△CDE的面积．

24．定义：在平面直角坐标系中，对于任意两点A(x₁，y₁)，B(x₂，y₂)，如果点C(x，y)满足x=x₁-x₂，y=y₁-y₂，那么称点C是点A，B的“双减点”．例如：A(3，2)，B(-1，5)，当点C(x，y)满足x=3-(-1)=4，y=2-5=-3，则称点C(4，-3)是点A，B的“双减点”．
(1)写出点A(-1，2)，B(2，-4)的“双减点”C的坐标，并且判断点C是否在直线AB上；
(2)点E(t，y₁)，F(t+1，y₂)，点G(x，y)是点E，F的“双减点”，是否存在非零实数k，使得点E，F，G均在函数y=的图象上，若存在，求实数k的值，若不存在，请说明理由；
(3)已知二次函数y=ax²+2bx-2(a＞b＞0)的图象经过点(2，6)，且与x轴交于点M(x₁，0)，N(x₂，0)，若点P为M，N的“双减点”，求点P与原点O的距离OP的取值范围．

25．如图，抛物线y=mx²-4mx+3m(m＞0)与x轴交于点A，B两点(点A在点B的左侧)，与y轴交于点C，抛物线的顶点坐标为D．
(1)求点A、点B的坐标；
(2)若△OAC∽△OCB，求m的值；
(3)若△ABD为正三角形，对于该抛物线上任意一点P(x₀，y₀)总有n+≥-my

2

0

-3y₀-4成立，求实数n的最小值．