17．先化简，再求值：÷(-)，其中．x=+2．

18．如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC，CF平分∠DCE．试探索CF与DE的位置关系，并说明理由．

19．攀枝花市某中学为了解学生对食堂工作的满意程度，9年级7班数学兴趣小组在全校甲、乙两个班内进行了调查统计，将调查结果分为不满意、一般、满意、非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．请结合图中信息，解决下列问题：

(1)求此次调查中接受调查的人数；
(2)求此次调查中结果为非常满意的人数；
(3)兴趣小组准备从调查结果为一般的4位同学中随机选择2位进行回访，已知4位同学中有2位来自甲班，另2位来自乙班，请用列表或用画树状图的方法求出选择的同学均来自甲班的概率．

20．某仓储中心有一个坡度为i=1：2的斜坡AB，顶部A处的高AC为4米，B、C在同一水平地面上，其横截面如图．
(1)求该斜坡的坡面AB的长度；
(2)现有一个侧面图为矩形DEFG的长方体货柜，其中长DE=2.5米，高EF=2米，该货柜沿斜坡向下时，点D离BC所在水平面的高度不断变化，求当BF=3.5米时，点D离BC所在水平面的高度DH．

21．如图，在平面直角坐标系中有Rt△ABC，∠BAC=90°，AB=AC，A(-3，0)，B(0，1)，C(m，n)．
(1)请直接写出C点坐标；
(2)将△ABC沿x轴的正方向平移t个单位，B、C两点的对应点B′、C′正好落在反比例函数y=在第一象限内图象上，请求出t与k的值；
(3)在(2)的条件下，问是否存在x轴上的点M和反比例函数y=图象上的点N，使得以B′、C′、M、N为顶点的四边形构成平行四边形？如果存在，请求出所有满足条件的点M和点N的坐标；如果不存在，请说明理由．

22．如图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E和点D，OB与⊙O交于点F，连接DF、DC．已知OA=OB，CA=CB．
(1)求证：直线AB是⊙O的切线；
(2)求证：∠FDC=∠EDC；
(3)已知：DE=10，DF=6，求DC的长．

23．在直角坐标系中，过原点O及点A(8，0)，C(0，6)作矩形OABC，连接OB，点D为OB的中点，点E是线段AB上的动点，连接DE，作DF⊥DE，交OA于点F，连接EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．

(1)如图1，当t=3时，求DF的长．
(2)如图2，当点E在线段AB上移动的过程中，的大小是否发生变化？如果变化，请说明理由；如果不变，请求出的值．
(3)连接AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．

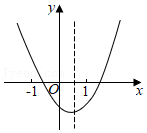
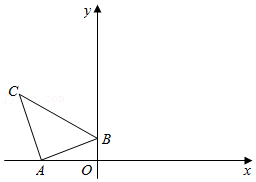
24．在平面直角坐标系中，过点A(3，4)的抛物线y=ax²+bx+4与x轴交于点B(-1，0)，与y轴交于点C，过点A作AD⊥x轴于点D．

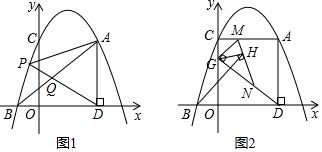
(1)求抛物线的解析式．
(2)如图1，点P是直线AB上方抛物线上的一个动点，连接PD交AB于点Q，连接AP，当S_△AQD=2S_△APQ时，求点P的坐标．
(3)如图2，G是线段OC上一个动点，连接DG，过点G作GM⊥DG交AC于点M，过点M作射线MN，使∠NMG=60°，交射线GD于点N；过点G作GH⊥MN，垂足为点H，连接BH．请直接写出线段BH的最小值．