


| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


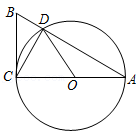
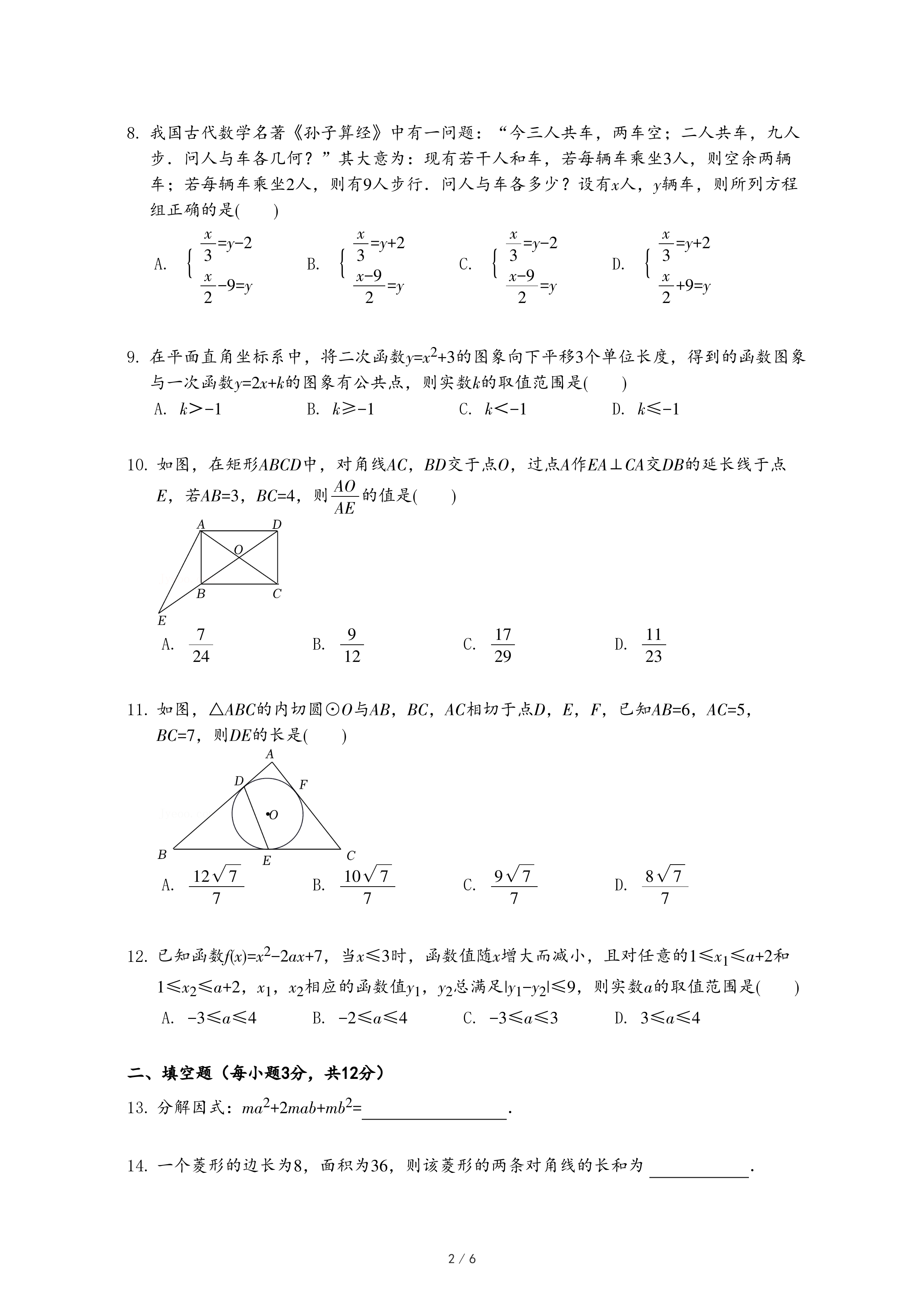
| AO |
| AE |
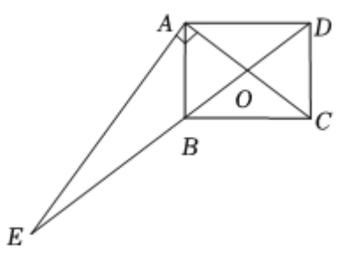
| 7 |
| 24 |
| 9 |
| 12 |
| 17 |
| 29 |
| 11 |
| 23 |
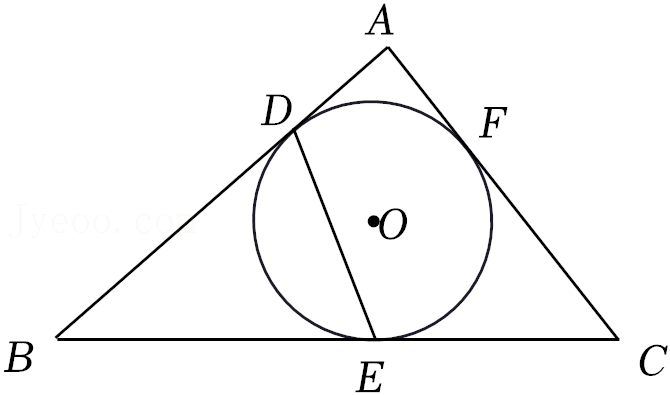
| 12 √7 |
| 7 |
| 10 √7 |
| 7 |
| 9 √7 |
| 7 |
| 8 √7 |
| 7 |
| 1 |
| 2 |
| x2-2x |
| x2-4 |
| x2+4x+4 |
| x+2 |
| 4+4x |
| x+2 |
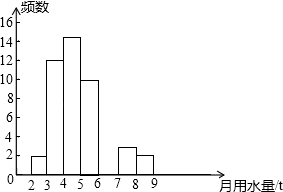
| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | ________ | ________ |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | ________ | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
| 甲型客车 | 乙型客车 | |
| 载客量(人/辆) | 35 | 30 |
| 租金(元/辆) | 400 | 320 |
| 6 |
| x |
| 6 |
| x |
| 6 |
| x |
| 6 |
| x |
| 1 |
| 2 |
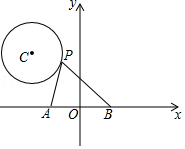
| AE |
| AP |