| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| y |
| x-y |
| x |
| y-x |


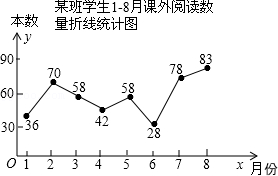
| 1 |
√x-3 |
| k |
| x |
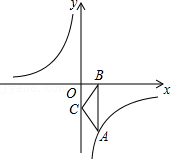
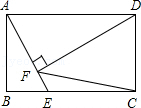
| 1 |
| 3 |
| x-3 |
| x2-1 |
| x2+2x+1 |
| x-3 |
| 1 |
| x-1 |
| 1 |
| 4 |
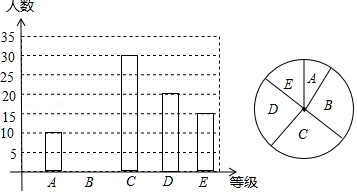
| 成绩 | 3′40″及以下 | 3′41~4′ | 4′01″~4′20′ | 4′21″~4′40″ | 4′41″及以上 |
| 等级 | A | B | C | D | E |
| 百分比 | 10% | 25% | m | 20% | n |
| 1 |
| x |
| x | … | -4 | -3 | -2 | -1 | -
| -
| -
|
|
|
| 1 | 2 | 3 | 4 | … | ||||||||||||||||||||||||
| y | … | -4
| -3
| -2
| -2 | -2
| -3
| -4
| 4
| 3
| 2
| 2 | 2
| 3
| 4
| … |
| 1 |
| x |
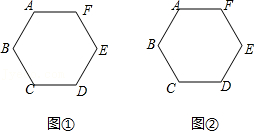
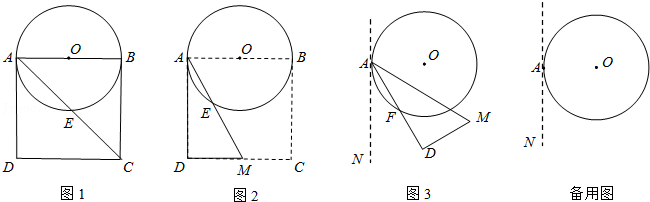
| DC |
| EB |

| DC |
| EB |
| DC |
| EB |
| DC |
| EB |
| DC |
| EB |