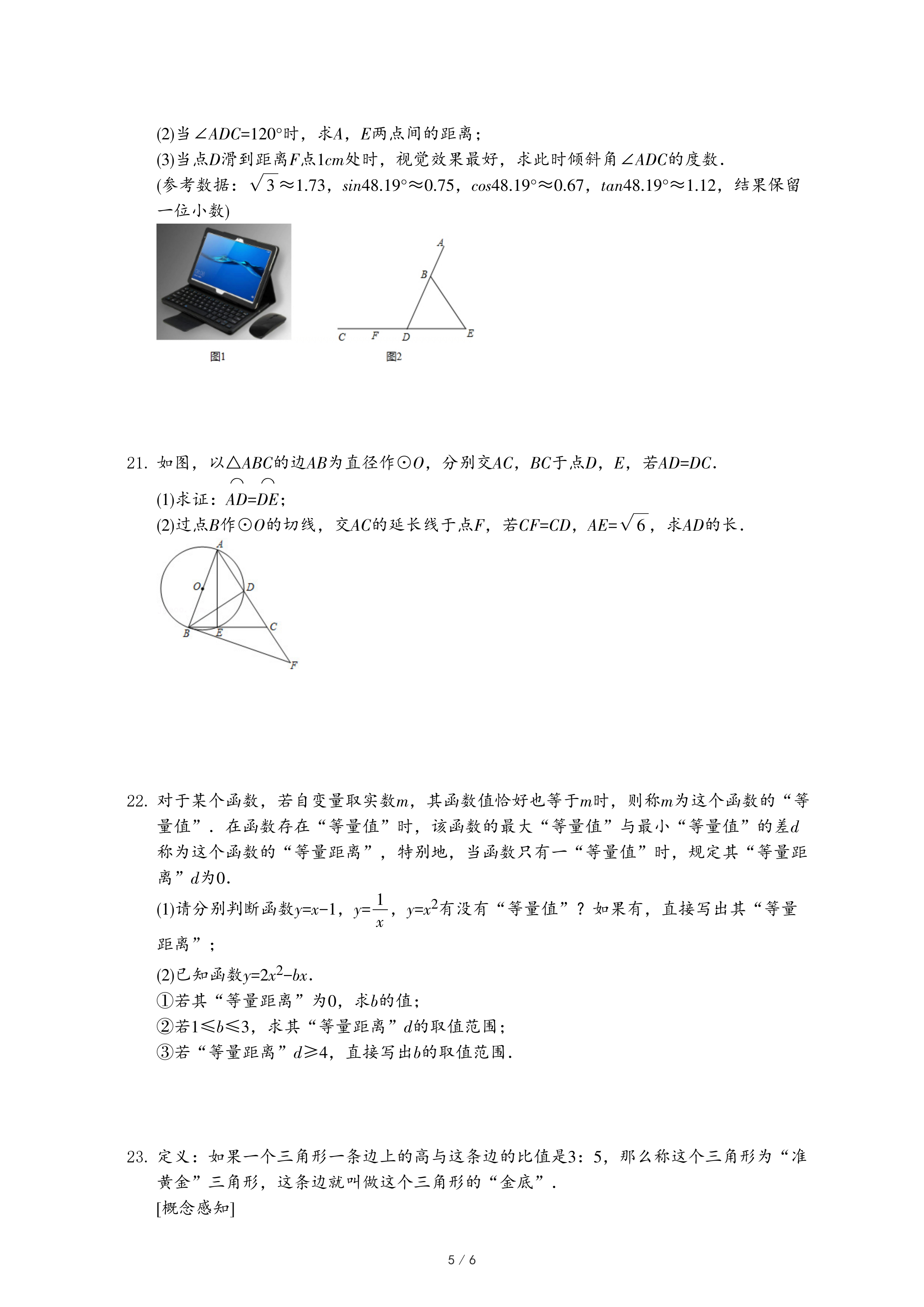
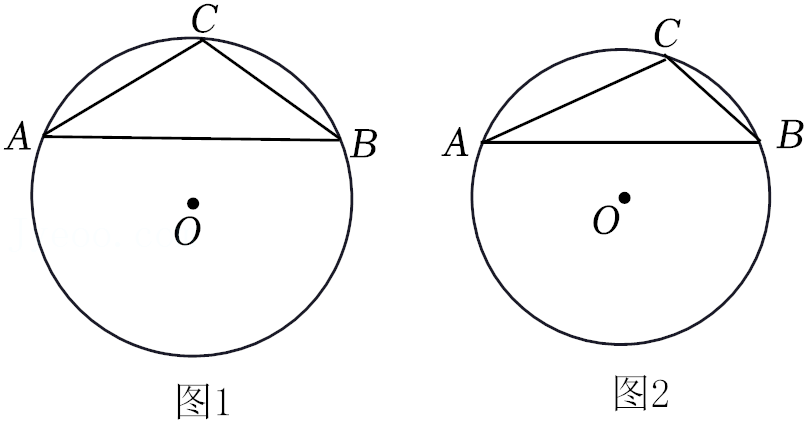
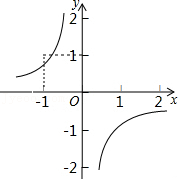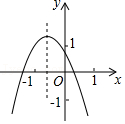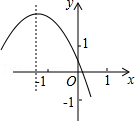23.定义:如果一个三角形一条边上的高与这条边的比值是3:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
[概念感知]
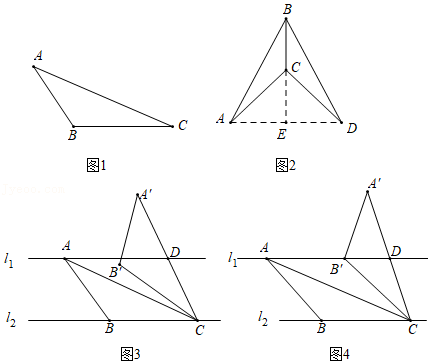
(1)如图1,在△ABC中,AC=12,BC=10,∠ACB=30°,试判断△ABC是否是“准黄金”三角形,请说明理由.
[问题探究]
(2)如图2,△ABC是“准黄金”三角形,BC是“金底”,把△ABC沿BC翻折得到△DBC,连接AD交BC的延长线于点E,若点C恰好是△ABD的重心,求
的值.
[拓展提升]
(3)如图3,l
1∥l
2,且直线l
1与l
2之间的距离为3,“准黄金”△ABC的“金底”BC在直线l
2上,点A在直线l
1上,
=
,若∠ABC是钝角,将△ABC绕点C按顺时针方向旋转α(0°<α<90°)得到△A'B'C,线段A'C交l
1于点D.
①当α=30°时,则CD=
;
②如图4,当点B'落在直线l
1上时,求
的值.