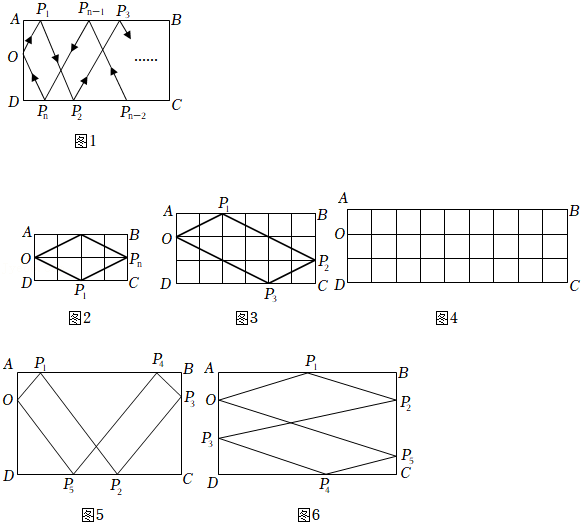
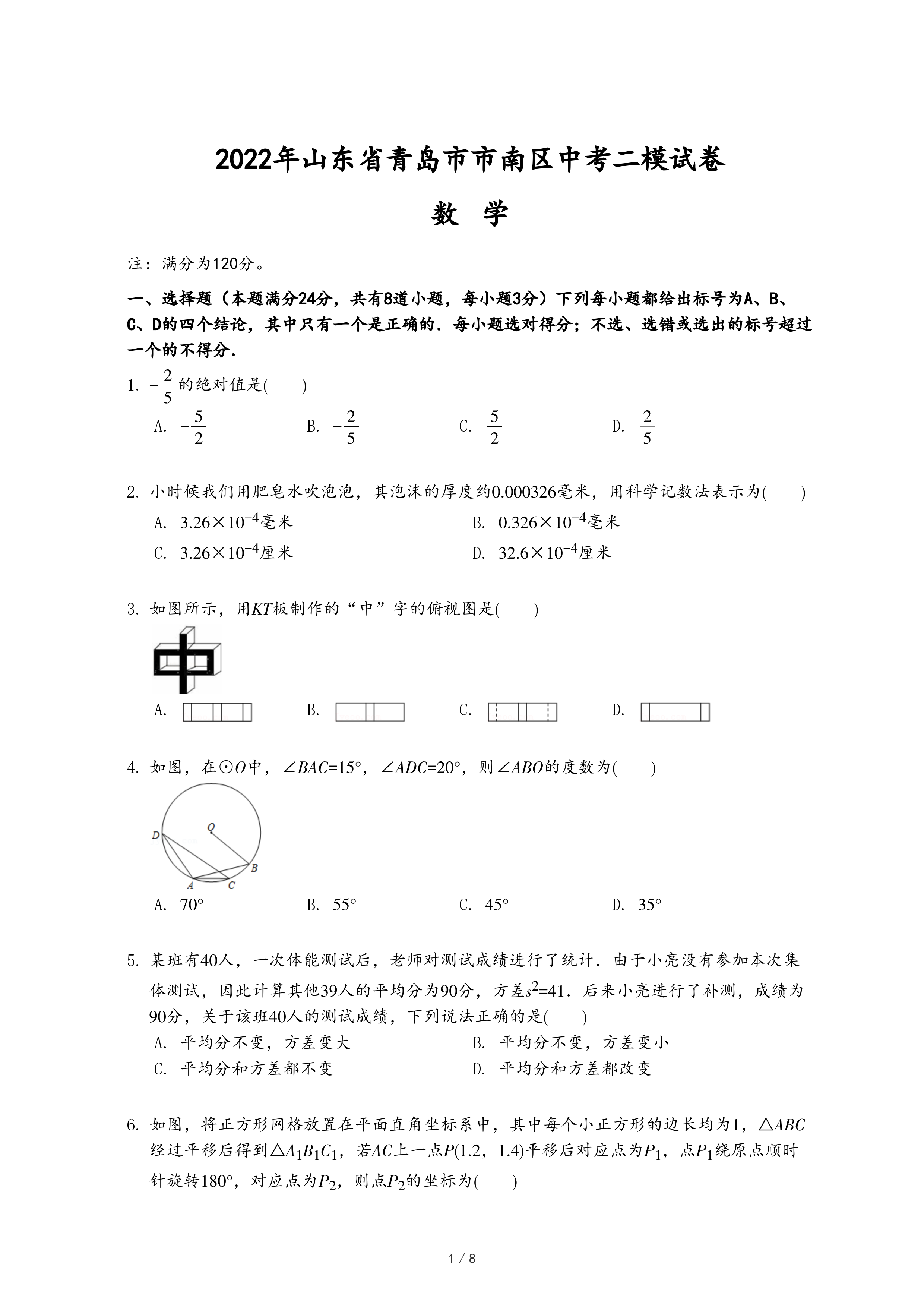
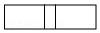
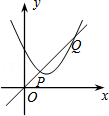
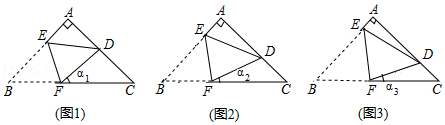
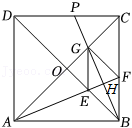
23.新定义:如图1,在长方形ABCD中,点O为AD边上的一点(不与A、D重合).若一个小球从点O出发,依次在长方形各边上经过n次反弹后恰好回到点O(反弹点分别为P
1、P
2、P
3、……、P
n,且每次反弹的入射角等于反射角).设此时的
=k,则称k的值为n次完美反弹比(n≥3且n为奇数).
设长方形ABCD中,AB=x,AD=y.
问题提出:当n=3时,k与x、y之间有什么等量关系呢?
探究1:设每个小正方形的边长均为1.
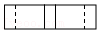
①如图2,在长方形ABCD中,x=4,y=2.若小球从格点O出发,依次在AB、BC、CD边上经过3次反弹后恰好回到点O,显然,此时k=2.
②如图3,在长方形ABCD中,x=6,y=3.若小球从格点O出发,依次在AB、BC、CD边上经过3次反弹后恰好回到点O,显然,此时k=2.
③如图4,在长方形ABCD中,x=9,y=3,若小球从格点O出发,依次在AB、BC、CD边上经过3次反弹后恰好回到点O,
(1)请在图3中用P
1、P
2、P
3标记每条边上的反弹点,并画出小球每次反弹的轨迹,再直接写出此时k=
.
……
问题解决1:
(2)通过归纳,n=3时,k与x、y间的等量关系为:
.
探究2:当n>3时,k与x、y之间又有什么等量关系呢?
(3)当n=5时,有图5、图6两种情况.请直接写出k与x、y之间所有可能的等量关系:
.
(4)请直接写出当n=7时,k与x、y之间所有可能的等量关系:
.
问题解决2:
(5)若长方形ABCD中,k为该长方形的n次完美反弹比(n>3且n为奇数),请直接写出k与n、x、y之间所有可能的等量关系:
.