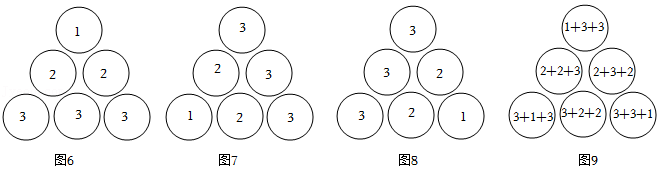
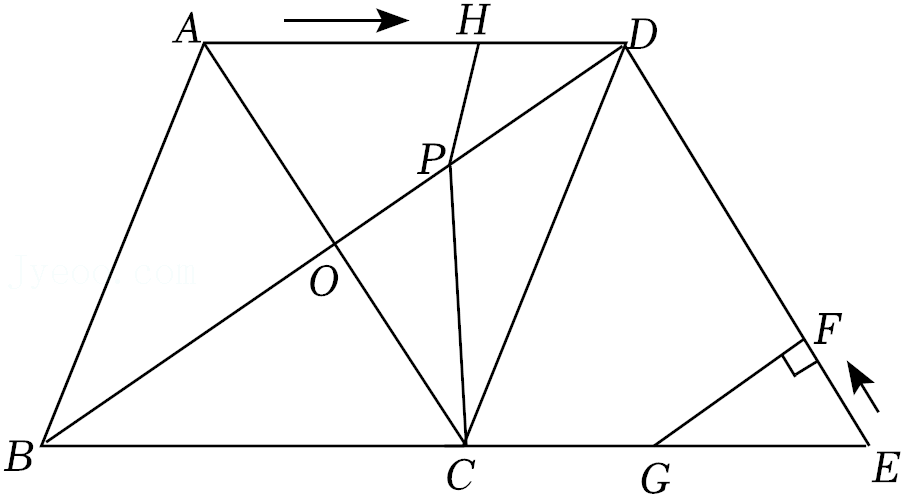
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |

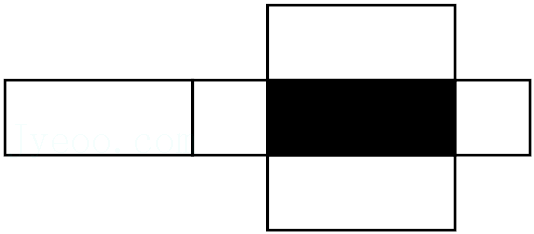
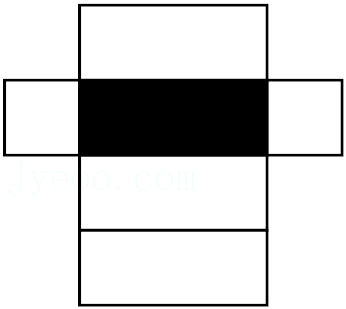




| 年龄(岁) | 14 | 15 | 16 | 17 | 18 |
| 人数 | 2 | 4 | 3 | 2 | 1 |
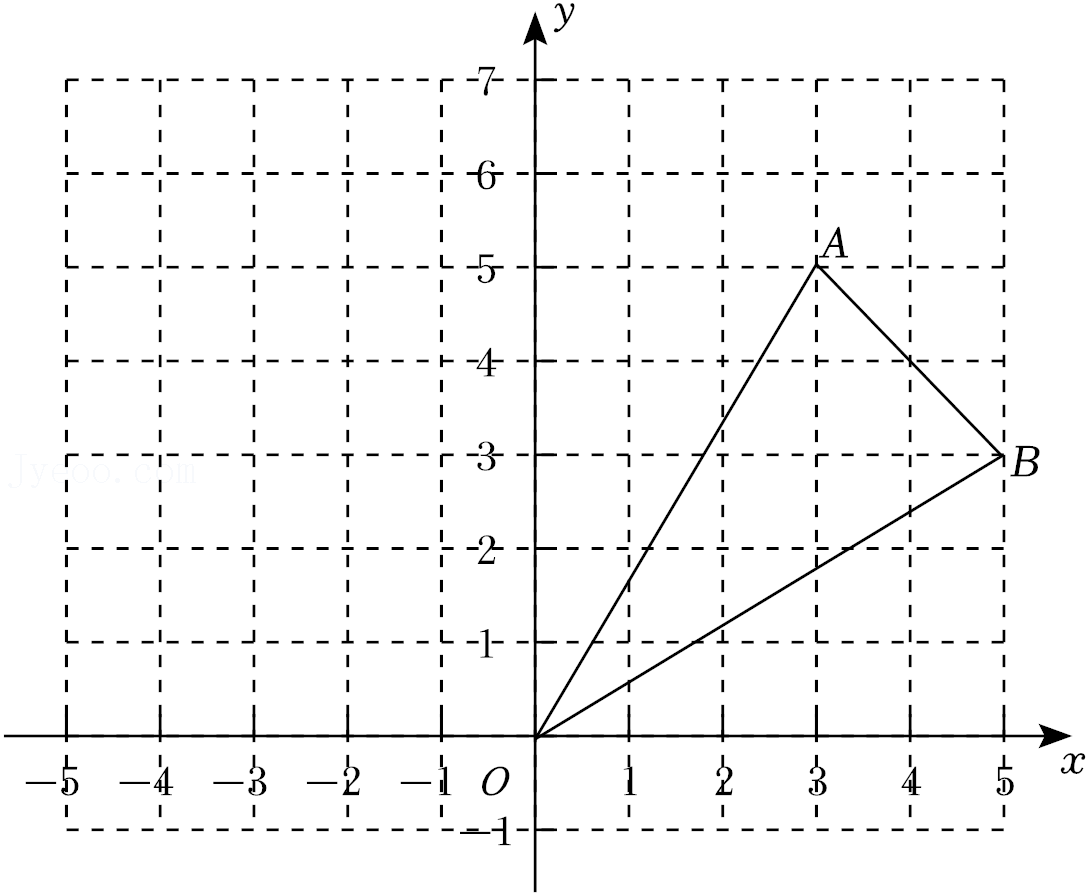
| 4 |
| 5 |
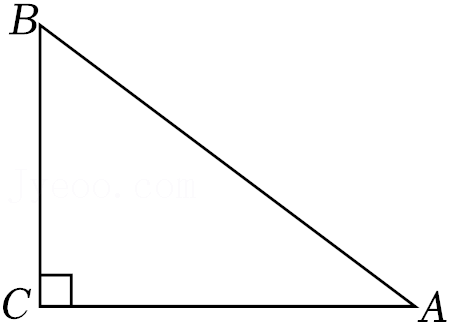
| x | … | -
| 0 | 2 | 3 | 4 | … | ||
| y1 | … |
| 1 | 3 | 4 | 5 | … | ||
| y2 | … |
| -2 | -2 | 4 | 14 | … |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
√5 -√20 |
√80 |
| 3 |
| 5 |
√3 |
| 2 |

| x-3 |
| x2-6x+9 |
| x2+3x |
| x+3 |
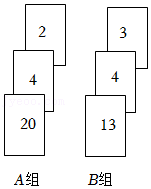
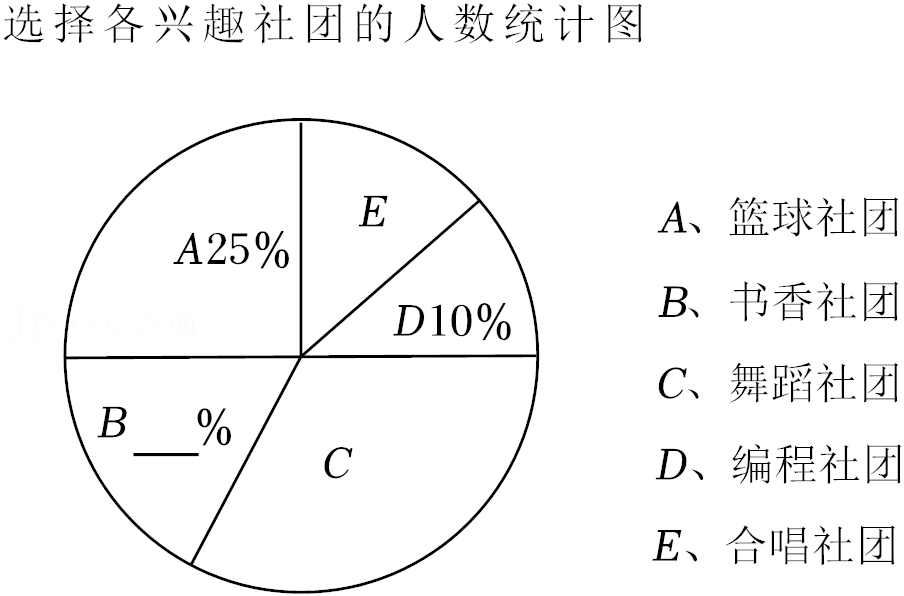
| 兴趣社团 | 人数 |
| A.篮球社团 | 10 |
| B.书香社团 | 8 |
| C.舞蹈社团 | a |
| D.编程社团 | 4 |
| E.合唱社团 | 6 |
| 19 |
| 20 |
| 29 |
| 100 |
| 10 |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
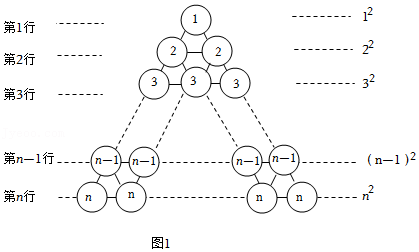
n个n |
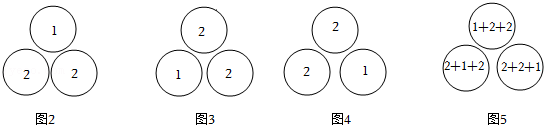
| 1 |
| 3 |
| 1 |
| 3 |