21.阅读理解:
我们把一条直线倾斜角α的正切值叫做这条直线的斜率,用小写字母k表示.一般的,直线y=kx+b(k≠0)中的k,叫做这条直线的斜率,则有k=
tanα.
探究发现:
某数学兴趣小组利用以上材料,通过多次验证和查阅资料探究得出:经过两点P(x
1,y
1),Q(x
2,y
2)(x
1≠x
2)的直线y=kx+b的斜率为:k
PQ=
.
启发应用:
(1)应用以上结论直接写出过A(2,3),B(-1,0)两点的直线AB的斜率k为
;
深入探究:
数学兴趣小组继续深入研究直线的“斜率”问题,得到结论:任意两条不和坐标轴平行的直线互相垂直时,这两条直线的斜率之积是定值.
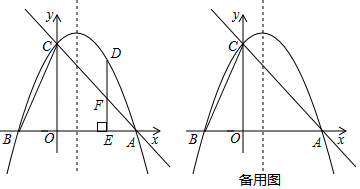
(2)①已知C(-6,0),D(3,6),E(0,3),F(6,-6),当直线CD与直线EF互相垂直时,请求出直线CD与直线EF的斜率之积;
②事实上,任意两条不和坐标轴平行的直线互相垂直时,这两条直线的斜率之积是定值,由①可知这个定值为
;
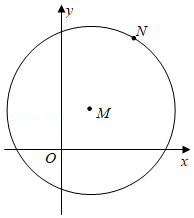
(3)如图,⊙M为以点M为圆心,MN的长为半径的圆.已知M(1,2),N(4,5),请结合(2)中的结论,求出过点N的⊙M的切线l的解析式.