19.为了积极响应中共中央文明办关于“文明用餐”的倡议,某校开展了“你的家庭使用公筷了吗?”的调查活动,并随机抽取了部分学生,对他们家庭用餐使用公筷情况进行统计,统计分类为以下四种:A(完全使用)、B(多数时间使用)、C(偶尔使用)、D(完全不使用),将数据进行整理后,绘制了两幅不完整的统计图.
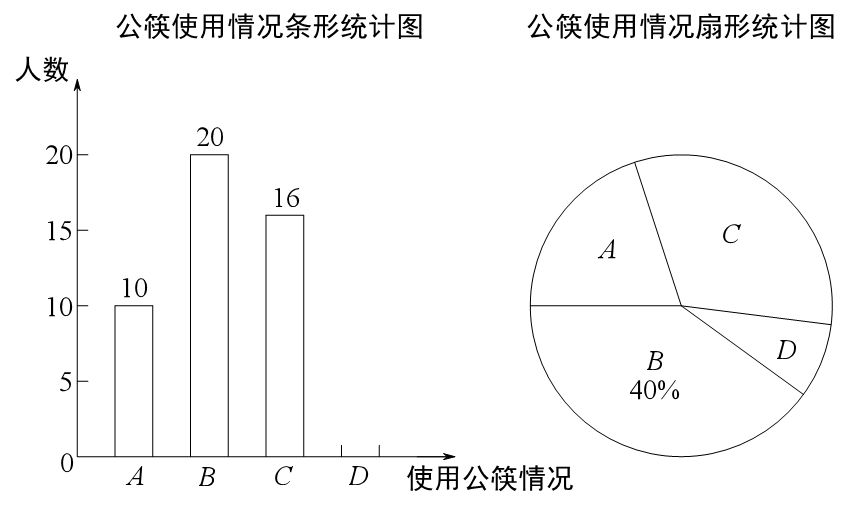
根据以上信息,解答下列问题:
(1)本次抽取的学生总人数共有
;
(2)补全条形统计图;
(3)扇形统计图中A对应的扇形的圆心角度数是
;
(4)为了了解少数学生完全不使用公筷的原因,学校决定从D组的学生中随机抽取两位进行回访,若D组中有3名男生,其余均为女生,请用列表法或画树状图的方法,求抽取的两位学生恰好是一男一女的概率.