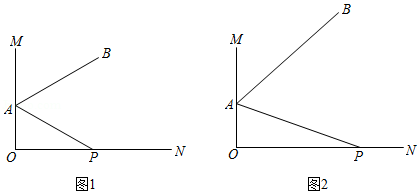25.品味诗词之美,传承中华文明,央视节目《中国诗词大会》备受大众欢迎.节目规则如下:由100位诗词爱好者组成的百人团与挑战者共同答题,每位挑战者最多可答五轮题.每轮比赛答题时,如挑战者答对,则百人团答错的人数即为选手该轮得分;如挑战者答错,则该轮不得分,且停止答题.每轮比赛的得分之和即为挑战者的总得分.现有甲、乙、丙三人作为挑战者参加节目答题,相关信息如下:
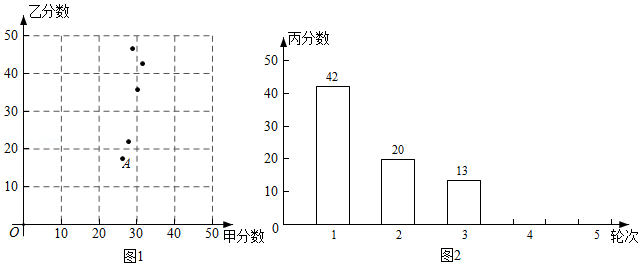
a.甲、乙两人参加比赛的得分统计图如图1,每个点的横坐标与纵坐标分别表示甲、乙二人在相同轮次的得分;
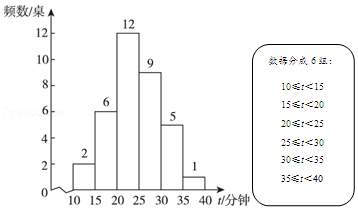
b.丙参加比赛的得分统计图如图2;
根据以上信息,回答下列问题:
(1)已知点A的坐标为(26,18),则此轮比赛中:甲的得分为
,与甲同场答题的百人团中,有
人答对;
(2)这五轮比赛中,甲得分高于乙得分的比赛共有
轮;甲、乙、丙三人中总得分最高的为
;
(3)设甲参加的第一轮至第五轮比赛时百人团答对人数的方差为s
12,乙参加的第一轮至第五轮比赛时百人团答对人数的方差为s
22,则s
12 s
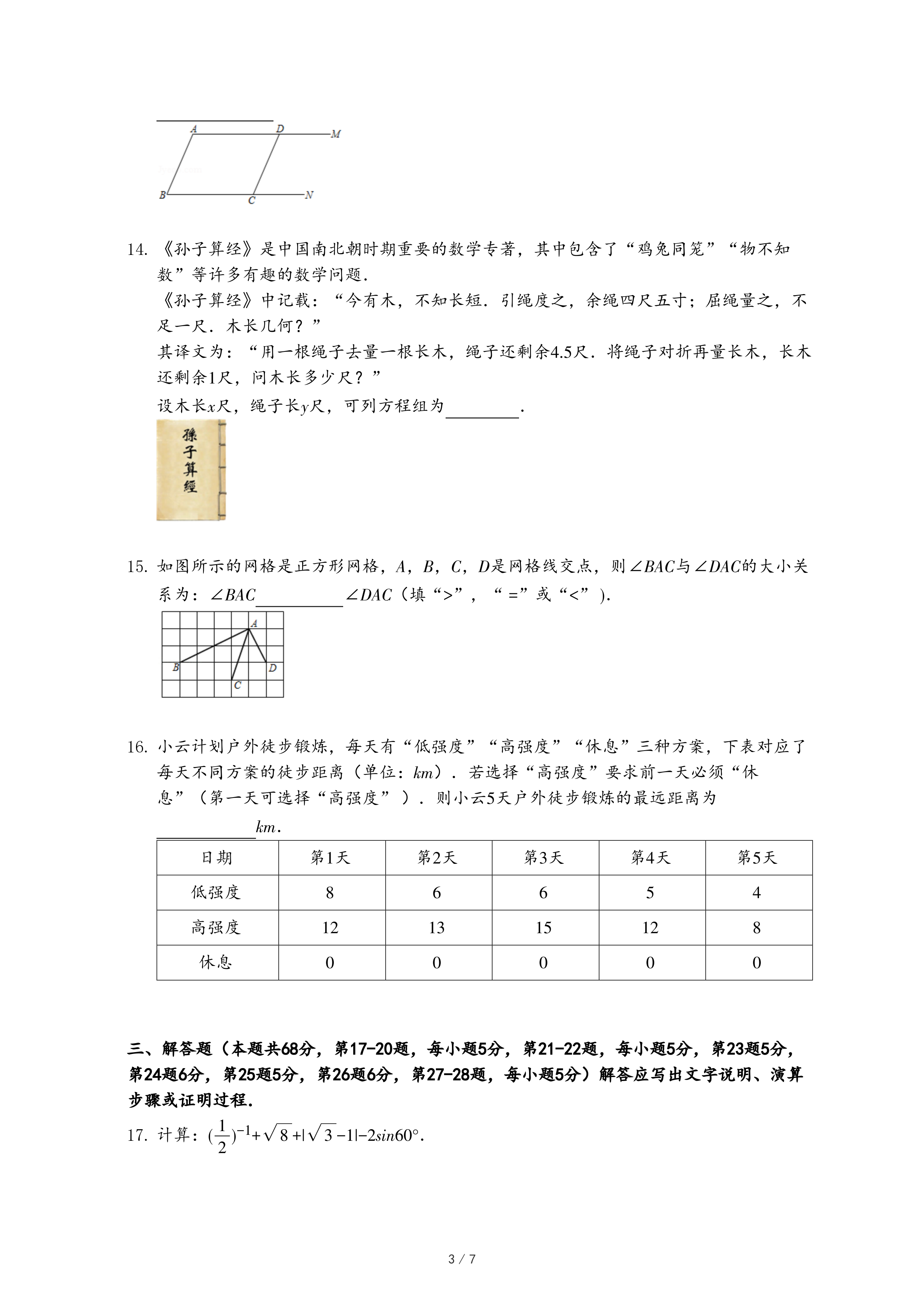
22(填“>”,“ <”或“=” ).