21.北京冬奥会正式比赛项目冬季两项是融滑雪和射击于一体的项目,要求运动负滑行一段时间再进行射击,对运动员的体能和稳定性都是极大的考验.某冬季两项集训队为了解运动员滑雪后射击的准确性,从甲、乙两个队分别抽了40名运动员进行了模拟测试,并将他们滑雪10公里后的射击成绩进行了整理、描述和分析,下面给出了部分信息.(说明:成绩8.0~10环及以上为优秀;7.0~7.9环为良好;6.0~6.9环为合格;6.0环以下为不合格).
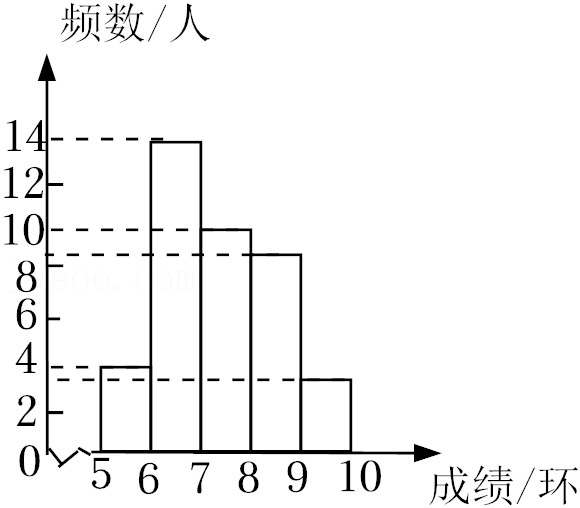
(1)甲队运动员成绩的频数分布直方图如图所示
(数据分为五组:5≤x<6;6≤x<7;7≤x<8;8≤x<9;9≤x≤10)
(2)甲队运动员射击成绩在7≤x<8这一组的是:7、7.1、7.3,7.3、7.3、7.4、7.6、7.7、7.8、7.9;
(3)乙队运动员的成绩中没有3人相同,其平均数、中位数、众数、优秀率如下:
| 平均数 | 中位数 | 众数 | 优秀率 |
| 7.9 | 7.6 | 8.4 | 40% |
根据以上信息,回答下列问题:
(1)求甲队运动员射击成绩在7≤x<8这组数据的中位数和众数;
(2)成绩是7.6环的运动员,在哪个队里的名次更好些?请说明理由;
(3)根据上述信息,推断
队运动员滑雪后射击状态状况更好,理由为
.
(至少从两个不同的角度说明推断的合理性)