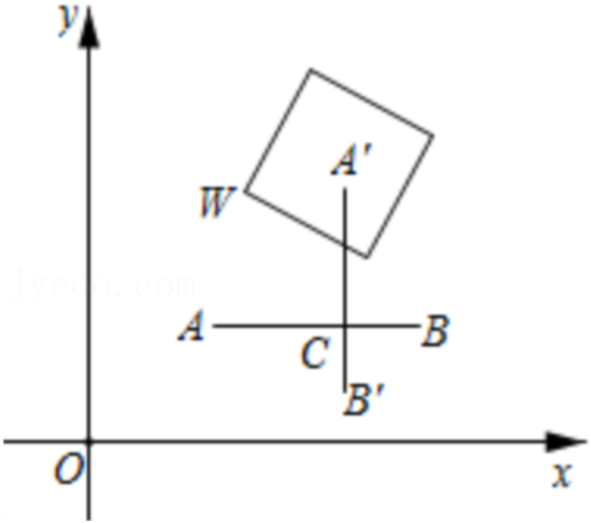
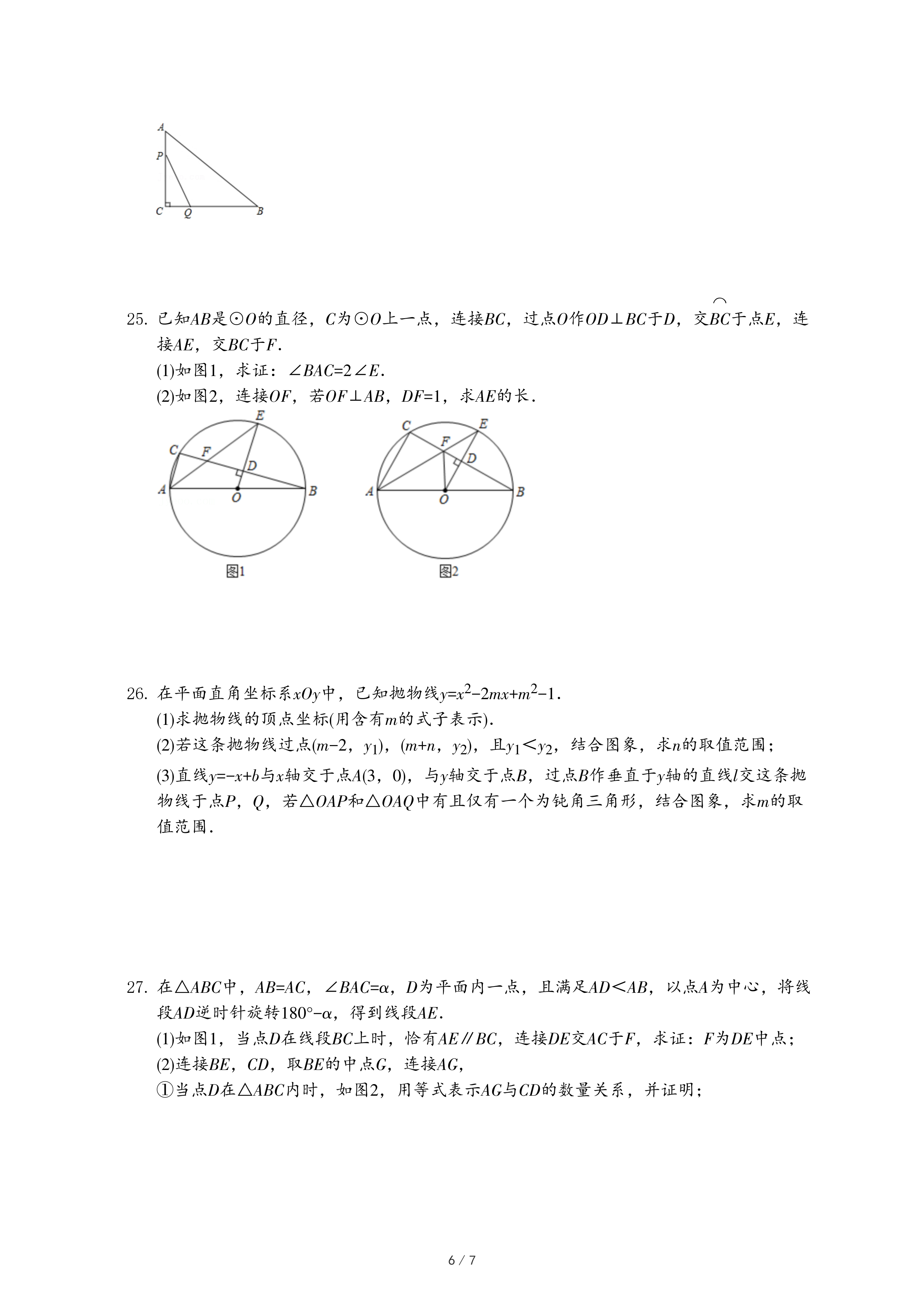
28.在平面直角坐标系xOy中,已知线段AB和图形W,如果对于给定的角α(0<α≤90°),存在线段AB上一点C,使得将线段AB绕点C顺时针旋转α角之后,所得到的线段与图形W有公共点,则称图形W是线段AB的α-联络图形.
例如,如图中的正方形即为线段AB的90°-联络图形.
已知点A(1,0),
(1)若点B的坐标为(3,0),直线y=-1是线段AB的α-联络图形,则α可能是下列选项中的
(填序号):
①15°
②30°
③54°
(2)若点B的坐标为(t,0),直线y=
x+
√3
是线段AB的60°-联络图形,求t的取值范围;
(3)若第一象限内的点B满足AB=2,点P(m,0),Q(m-1,
√3
),若存在某个点B,以及某个α,使得线段PQ是线段AB的α-联络图形,直接写出m的取值范围.