17．计算：|-3|-2tan60°+()^-1+．

18．解不等式组：．

19．已知a²-ab=1，求代数式(a-b)²+(a+b)(a-b)的值．

20．已知：如图，△ABC为锐角三角形，AB=AC．
求作：点P，使得AP=AB，且∠APC=∠BAC．
作法：①以点A为圆心，AB长为半径画圆；
②以点B为圆心，BC长为半径画弧，交⊙A于点D(异于点C)；
③连接DA并延长交⊙A于点P．
所以点P就是所求作的点．
(1)使用直尺和圆规，依作法补全图形(保留作图痕迹)；
(2)完成下面的证明．
证明：连接PC．
∵AB=AC，
∴点C在⊙A上．
∵⌒DC=⌒DC，
∴∠DPC=∠DAC(       )(填推理的依据)，
由作图可知，⌒BD=⌒BC，
∴∠DAB=      =∠DAC．
∴∠APC=∠BAC．

21．已知一次函数y₁=2x+m的图象与反比例函数y₂=(k＞0)的图象交于A，B两点．
(1)当点A的坐标为(2，1)时：
①求m，k的值；②当x＞2时，y₁      y₂(填“＞”“=”或“＜”)．
(2)将一次函数y₁=2x+m的图象沿y轴向下平移4个单位长度后，使得点A，B关于原点对称，求m的值．

22．如图，在△ABC中，AB=BC，BD平分∠ABC交AC于点D，点E为AB的中点，连接DE，过点E作EF∥BD交CB的延长线于点F．
(1)求证：四边形DEFB是平行四边形；
(2)当AD=4，BD=3时，求CF的长．

23．如图1是某条公路的一个单向隧道的横断面．经测量，两侧墙AD和BC与路面AB垂直，隧道内侧宽AB=4米．为了确保隧道的安全通行，工程人员在路面AB上取点E，测量点E到墙面AD的距离和到隧道顶面的距离EF．设AE=x米，EF=y米．
通过取点、测量，工程人员得到了x与y的几组值，如表：

(1)隧道顶面到路面AB的最大高度为       米；
(2)请你帮助工程人员建立平面直角坐标系，描出表中各对对应值为坐标的点，画出可以表示隧道顶面的图象．

(3)今有宽为2.4米，高为3米的货车准备在隧道中间通过(如图2)．根据隧道通行标准，其车厢最高点到隧道顶面的距离应大于0.5米，结合所画图象，请判断该货车是否安全通过：      (填写“是”或“否”)．

24．2021年，我国粮食总产量再创新高．小刘同学登录国家统计局网站，查询到了我国2021年31个省、直辖市、自治区的粮食产量数据(万吨)，并对数据进行整理、描述和分析．下面给出了部分信息．
a．反映2021年我国31个省、直辖市、自治区的粮食产量数据频数分布直方图如图(数据分成8组：0≤x＜1000，1000≤x＜2000，2000≤x＜3000，3000≤x＜4000，4000≤x＜5000，5000≤x＜6000，6000≤x＜7000，7000≤x≤8000)：

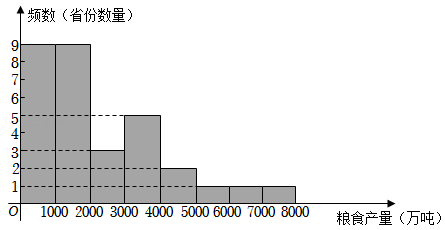
b.2021年我国各省、直辖市、自治区的粮食产量在1000≤x＜2000这一组的是：
1092.8，1094.9，1231.5，1270.4，1279.9，1386.5，1421.2，1735.8，1930.3
(1)2021年我国各省、直辖市、自治区粮食产量的中位数为       万吨；
(2)小刘同学继续收集数据的过程中，发现北京市与河南省的单位面积粮食产量(千克/公顷)比较接近，如图所示，他将自2016年至2021年北京市与河南省的单位面积粮食产量表示粮食总产量出来：(单位面积粮食产量=)
自2016-2021年间，设北京市单位面积粮食产量的平均值为x_A，方差为S

2

A

；河南省单位面积粮食产量的平均值为x_B，方差为S

2

B

；则x_A      x_B，S

2

A

      S

2

B

(填写“＞”或“＜”)；
(3)国家统计局公布，2021年全国粮食总产量13657亿斤，比上一年增长2.0%．如果继续保持这个增长率，计算2022年全国粮食总产量约为多少亿斤(保留整数)．

25．如图1，AB是⊙O的直径，点C是⊙O上不同于A，B的点，过点C作⊙O的切线与BA的延长线交于点D，连结AC，BC．
(1)求证：∠DCA=∠B；
(2)如图2，过点C作CE⊥AB于点E，交⊙O于点F，FO的延长线交CB于点G．若⊙O的直径为4，∠D=30°，求线段FG的长．

26．已知抛物线y=ax²-4ax+2(a≠0)过A(-1，m)，B(2，n)，C(3，p)三点．
(1)求n的值(用含有a的代数式表示)；
(2)若mnp＜0，求a的取值范围．

27．如图，在Rt△ACB中，∠ACB=90°，AC=BC．点D是BC延长线上一点，连接AD．将线段AD绕点A逆时针旋转90°，得到线段AE．过点E作EF∥BD，交AB于点F．
(1)①直接写出∠AFE的度数是       ；
②求证：∠DAC=∠E；
(2)用等式表示线段AF与DC的数量关系，并证明．

28．在平面直角坐标系xOy中，给出如下定义：点P为图形G上任意一点，将点P到原点O的最大距离与最小距离之差定义为图形G的“全距”，特别地，点P到原点O的最大距离与最小距离相等时，规定图形G的“全距”为0．
(1)如图，点A(-，1)，B(，1)．
①原点O到线段AB上一点的最大距离为       ，最小距离为       ；
②当点C的坐标为(0，m)时，且△ABC的“全距”为1，求m的取值范围；
(2)已知OM=2，等边△DEF的三个顶点均在半径为1的⊙M上．请直接写出△DEF的“全距”d的取值范围．