




| 1 |
| 2 |
| 3 √2 |
| 2 |
| 60 |
| x |
| 60 |
| 2x |
| 60 |
| x |
| 60 |
| 1.2x |
| 60 |
| x |
| 60 |
| 2x |
| 60 |
| 1.2x |
| 60 |
| x |
| 10 |
| x |
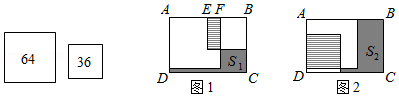
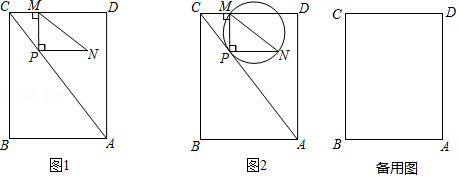
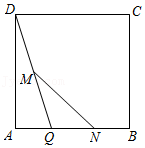
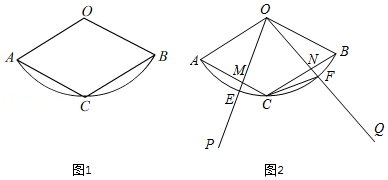
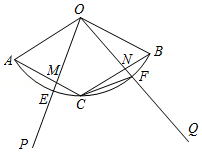
| ① | 以A为圆心,AB长为半径画弧交AD于点M; | ||
| ② | 分别以M,B为圆心,以大于
| ||
| ③ | 画射线AP交CB于点E,交DC的延长线于点F,连接ME. |
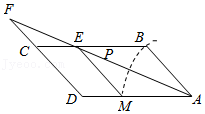
| BE |
| CE |
| CF |
| FD |
| 1 |
| 3 |
| 9 |
| 10 |
| 1 |
| 2 |
| 5 |
| 2 |
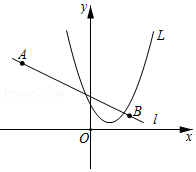
| a |
| 2 |
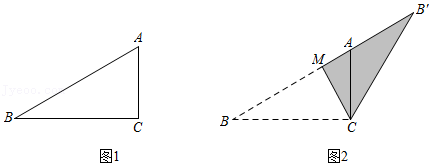
| 1 |
| 2 |
| 4x-4 |
| x |
| x-2 |
| x2 |
| 配发量/个 | 30 | 25 | 20 | 15 |
| 天数/天 | 2 | x | y | 1 |
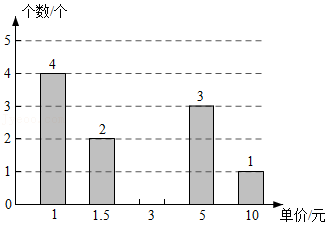
| 4 |
| 9 |
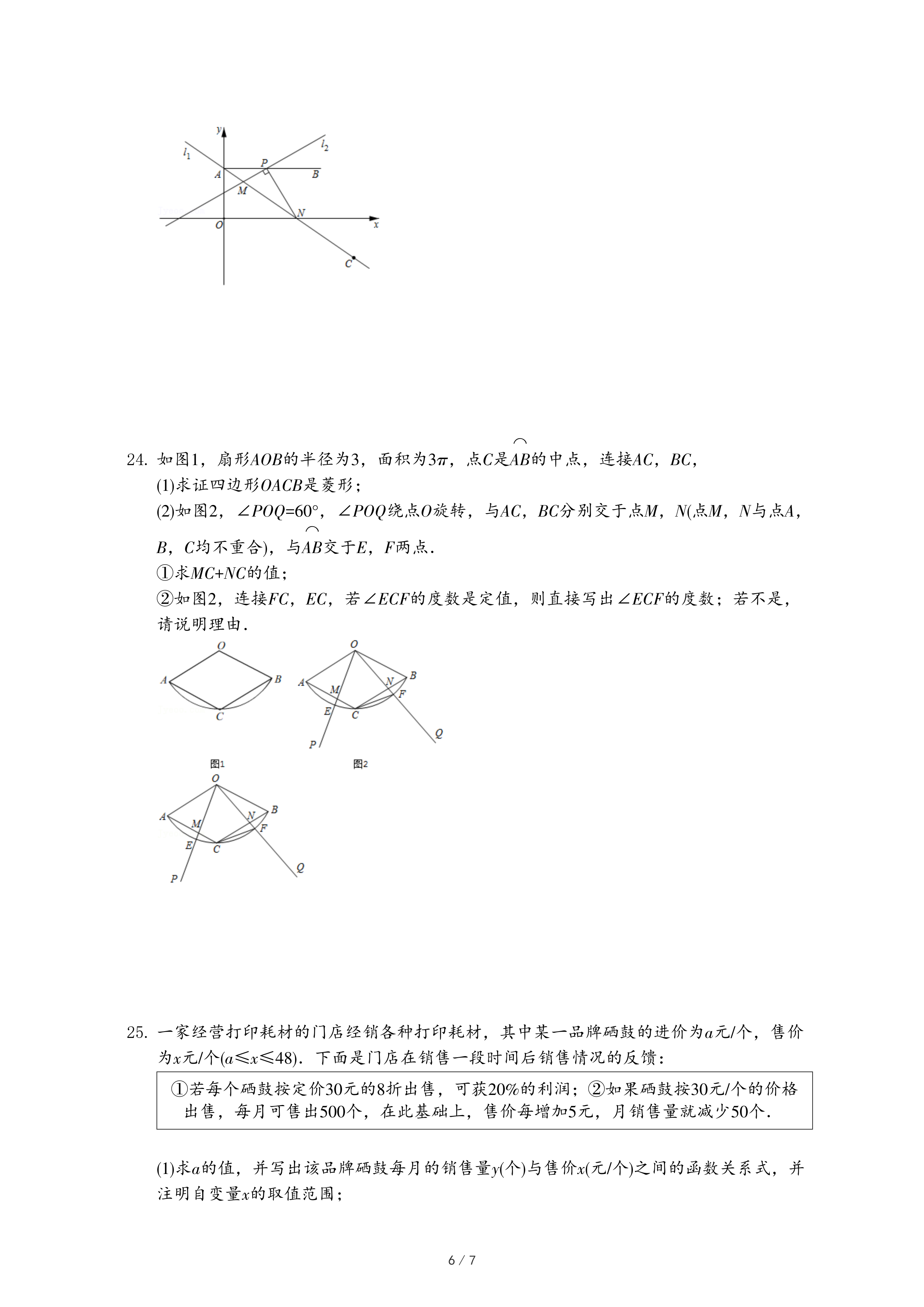
| ①若每个硒鼓按定价30元的8折出售,可获20%的利润;②如果硒鼓按30元/个的价格出售,每月可售出500个,在此基础上,售价每增加5元,月销售量就减少50个. |
| 3 |
| 4 |