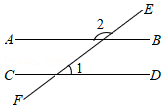
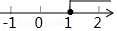30.阅读与理解:
三角形的中线的性质:三角形的中线等分三角形的面积,
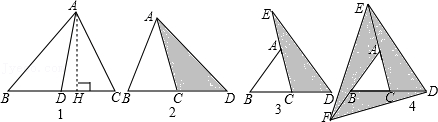
即如图1,AD是△ABC中BC边上的中线,
则S
△ABD=S
△ACD=
S
△ABC.
理由:∵BD=CD,∴S
△ABD=
BD×AH=
CD×AH=S
△ACD=
S
△ABC,
即:等底同高的三角形面积相等.
操作与探索
在如图2至图4中,△ABC的面积为a.
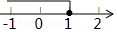
(1)如图2,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S
1,则S
1=
(用含a的代数式表示);
(2)如图3,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S
2,则S
2=
(用含a的代数式表示),并写出理由;
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图4).若阴影部分的面积为S
3,则S
3=
(用含a的代数式表示).
拓展与应用
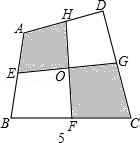
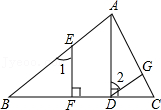
(4)如图5,已知四边形ABCD的面积是a,E、F、G、H分别是AB、BC、CD、DA的中点,求图中阴影部分的面积?