17．计算：(+1)+()²+|1-|

18．解方程：x²-2x-3=0．

19．下面是小亮设计的“过圆上一点作已知圆的切线”的尺规作图过程．
已知：点A在⊙O上．
求作：直线PA和⊙O相切．
作法：如图，
①连接AO；
②以A为圆心，AO长为半径作弧，与⊙O的一个交点为B；
③连接BO；
④以B为圆心，BO长为半径作圆；
⑤作⊙B的直径OP；
⑥作直线PA．所以直线PA就是所求作的⊙O的切线．
根据小亮设计的尺规作图过程，
(1)使用直尺和圆规依作法补全图形(保留作图痕迹)；
(2)完成下面的证明；
证明：在⊙O中，连接BA，
∵OA=OB，AO=AB，
∴OB=AB．
∴点A在⊙B上．
∵OP是⊙B的直径，
∴∠OAP=90°(      )(填推理的依据)．
∴OA⊥AP．
又∵点A在⊙O上，
∴PA是⊙O的切线(      )(填推理的依据)．

20．已知关于x的一元二次方程x²-3kx+2k²=0．
(1)求证：该方程总有两个实数根；
(2)若k＞0，且该方程的两个实数根的差为1，求k的值．

21．在平面直角坐标系xOy中，抛物线y=x²+mx+n经过点A(-3，0)，B(1，0)．
(1)求抛物线的解析式；
(2)设抛物线与y轴的交点为C，求△ABC的面积．

22．小宇和小伟玩“石头、剪刀、布”的游戏．这个游戏的规则是：“剪刀”胜“布”，“布”胜“石头”，石头”胜“剪刀”，手势相同不分胜负．如果二人同时随机出手(分别出三种手势中的一种手势)一次，那么小宇获胜的概率是多少？

23．某校举办了“冰雪运动进校园”活动，计划在校园一块矩形的空地上铺设两块完全相同的矩形冰场，如图所示，已知空地长27m，宽12m，矩形冰场的长与宽的比为4：3，如果要使冰场的面积是原空地面积的，并且预留的上、下通道的宽度相等，左、中、右通道的宽度相等，那么预留的上、下通道的宽度和左、中、右通道的宽度分别是多少米？

24．如图，AB是⊙O的直径，PA，PC是⊙O的切线，A，C是切点，连接AC，PO，交点为D．
(1)求证：∠BAC=∠OPC；
(2)延长PO交⊙O于点E，连接BE，CE．若∠BEC=30°，PA=8，求AB的长．

25．小朋在学习过程中遇到一个函数y=|x|(x-3)²．
下面是小朋对其探究的过程，请补充完整：
(1)观察这个函数的解析式可知，x的取值范围是全体实数，并且y有       值(填“最大”或“最小”)，这个值是       ；
(2)进一步研究，当x≥0时，y与x的几组对应值如表：

结合上表，画出当x≥0时，函数y=|x|(x-3)²的图象；
(3)结合(1)(2)的分析，解决问题：
若关于x的方程|x|(x-3)²=kx-1有一个实数根为2，则该方程其它的实数根约为       (结果保留小数点后一位)．

26．在平面直角坐标系xOy中，P(x₁，y₁)，Q(x₂，y₂)是抛物线y=x²-2mx+m²-1上任意两点．
(1)求抛物线的顶点坐标(用含m的式子表示)；
(2)若x₁=m-2，x₂=m+2，比较y₁与y₂的大小，并说明理由；
(3)若对于-1≤x₁＜4，x₂=4，都有y₁≤y₂，直接写出m的取值范围．

27．如图，在△ABC中，AB=AC，∠BAC=90°，D是边BC上一点，作射线AD，满足0°＜∠DAC＜45°，在射线AD取一点E，且AE＞BC．将线段AE绕点A逆时针旋转90°得到线段AF，连接BE，FE，连接FC并延长交BE于点G．
(1)依题意补全图形；
(2)求∠EGF的度数；
(3)连接GA，用等式表示线段GA，GB，GC之间的数量关系，并证明．

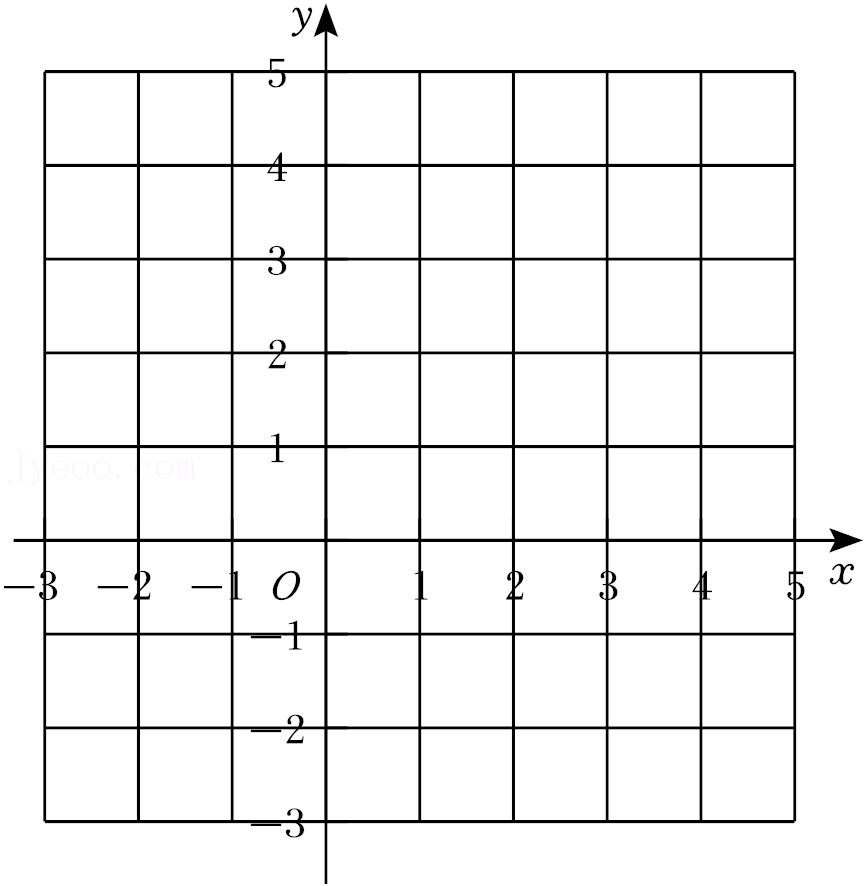
28．对于平面直角坐标系xOy中的图形M，N，给出如下定义：若图形M和图形N有且只有一个公共点P，则称点P是图形M和图形N的“关联点”．
已知点A(2，0)，B(0，2)，C(2，2)，D(1，)．
(1)直线l经过点A，⊙B的半径为2，在点A，C，D中直线l和⊙B的“关联点”是       ；
(2)G为线段OA中点，Q为线段DG上一点(不与点D，G重合)，若⊙Q和△OAD有“关联点”，求⊙Q半径r的取值范围；
(3)⊙T的圆心为点T(0，t)(t＞0)，半径为t，直线m过点A且不与x轴重合．若⊙T和直线m的“关联点”在直线y=x+b上，请直接写出b的取值范围．