25.今年7月1日是中国共产党建党100周年纪念日,为了让学生进一步了解中国共产党的历史,某学校组织了一系列“党史知识”专题学习活动,对八年级甲,乙两班各40名学生进行了“党史”相关知识的测试,并分别抽取了15份成绩,并对成绩(百分制并取整数)进行整理、描述和分析,部分信息如下:
a.甲班、乙班15名学生测试成绩统计如下:
甲班:68,72,89,85,82,85,74,92,80,85,78,85,69,76,80.
乙班:86,89,83,76,73,78,67,80,80,79,80,84,82,80,83.
b.甲班15名学生测试成绩的频数分布直方图(不完整);
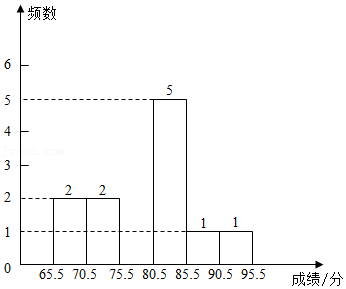
c.乙班15名学生测试成绩的频数分布表:
| 组别 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
| 乙 | 1 | 1 | a | b | 2 | 0 |
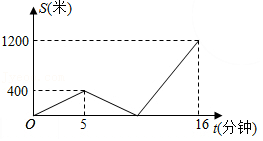
d.甲班、乙班15名学生测试成绩的平均数、众数、中位数和方差如表:
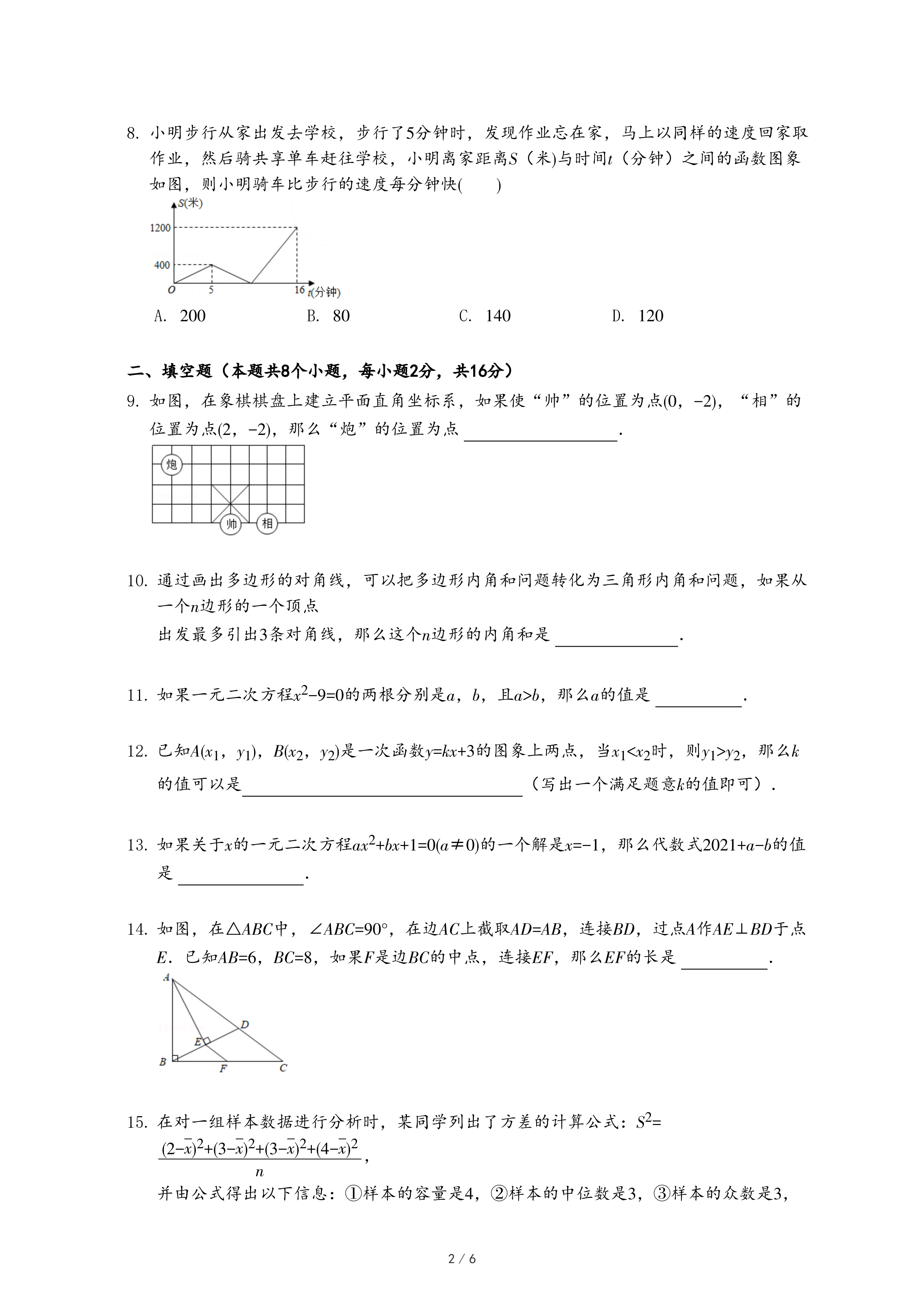
| 班级 | 平均数 | 众数 | 中位数 | 方差 |
| 甲 | 80 | x | 80 | 47.6 |
| 乙 | 80 | 80 | y | 26.2 |
根据以上信息,回答下列问题.
(1)补全甲班测试成绩的频数分布直方图;
(2)在乙班15名学生测试成绩的频数分布表中,a=
,b=
,
(3)在甲班、乙班15名学生测试成绩的平均数、众数、中位数、方差表中,x=
,y=
.
(4)你认为哪个班的学生掌握“党史”相关知识的整体水平较好,说明理由.