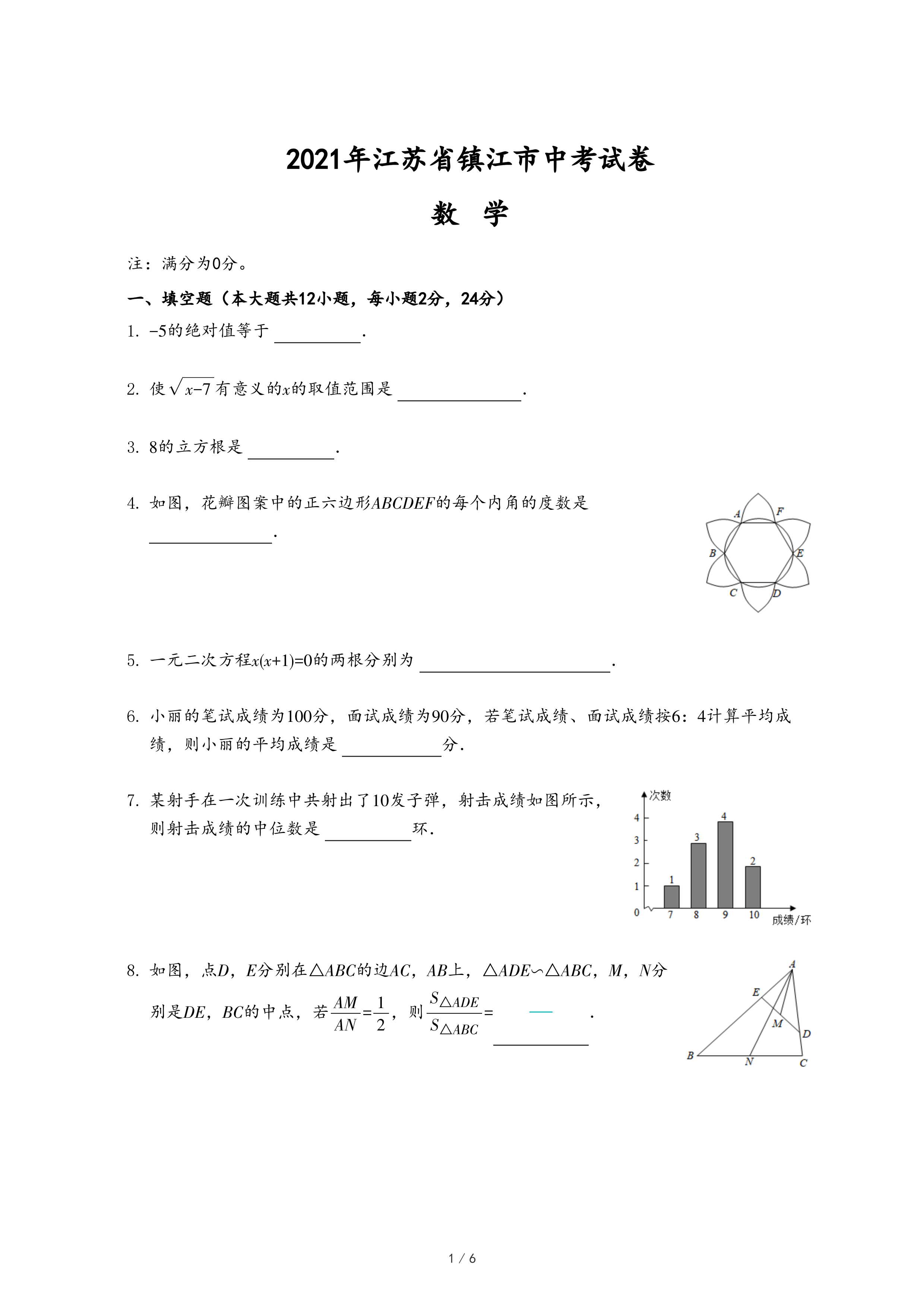
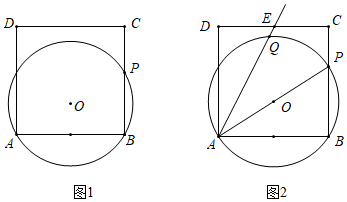
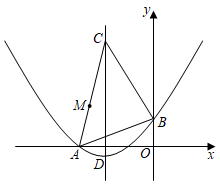
28.如图1,∠A=∠B=∠C=∠D=∠E=∠F=90°,AB,FE,DC为铅直方向的边,AF,ED,BC为水平方向的边,点E在AB,CD之间,且在AF,BC之间,我们称这样的图形为“L图形”,记作“L图形ABCDEF”.若直线将L图形分成面积相等的两个图形,则称这样的直线为该L图形的面积平分线.
【活动】
小华同学给出了图1的面积平分线的一个作图方案:如图2,将这个L图形分成矩形AGEF、矩形GBCD,这两个矩形的对称中心O
1,O
2所在直线是该L图形的面积平分线.
请用无刻度的直尺在图1中作出其他的面积平分线.(作出一种即可,不写作法,保留作图痕迹)
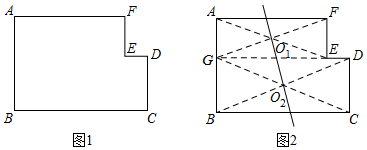
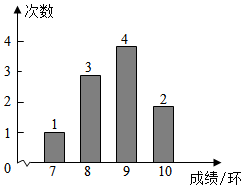
【思考】
如图3,直线O
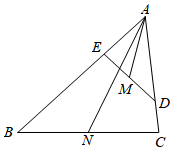
1O
2是小华作的面积平分线,它与边BC,AF分别交于点M,N,过MN的中点O的直线分别交边BC,AF于点P,Q,直线PQ
(填“是”或“不是”)L图形ABCDEF的面积平分线.
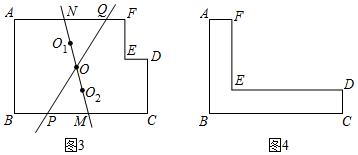
【应用】
在L图形ABCDEF形中,已知AB=4,BC=6.
(1)如图4,CD=AF=1.
①该L图形的面积平分线与两条水平的边分别相交于点P,Q,求PQ长的最大值;
②该L图形的面积平分线与边AB,CD分别相交于点G,H,当GH的长取最小值时,BG的长为
.
(2)设
=t(t>0),在所有的与铅直方向的两条边相交的面积平分线中,如果只有与边AB,CD相交的面积平分线,直接写出t的取值范围
.