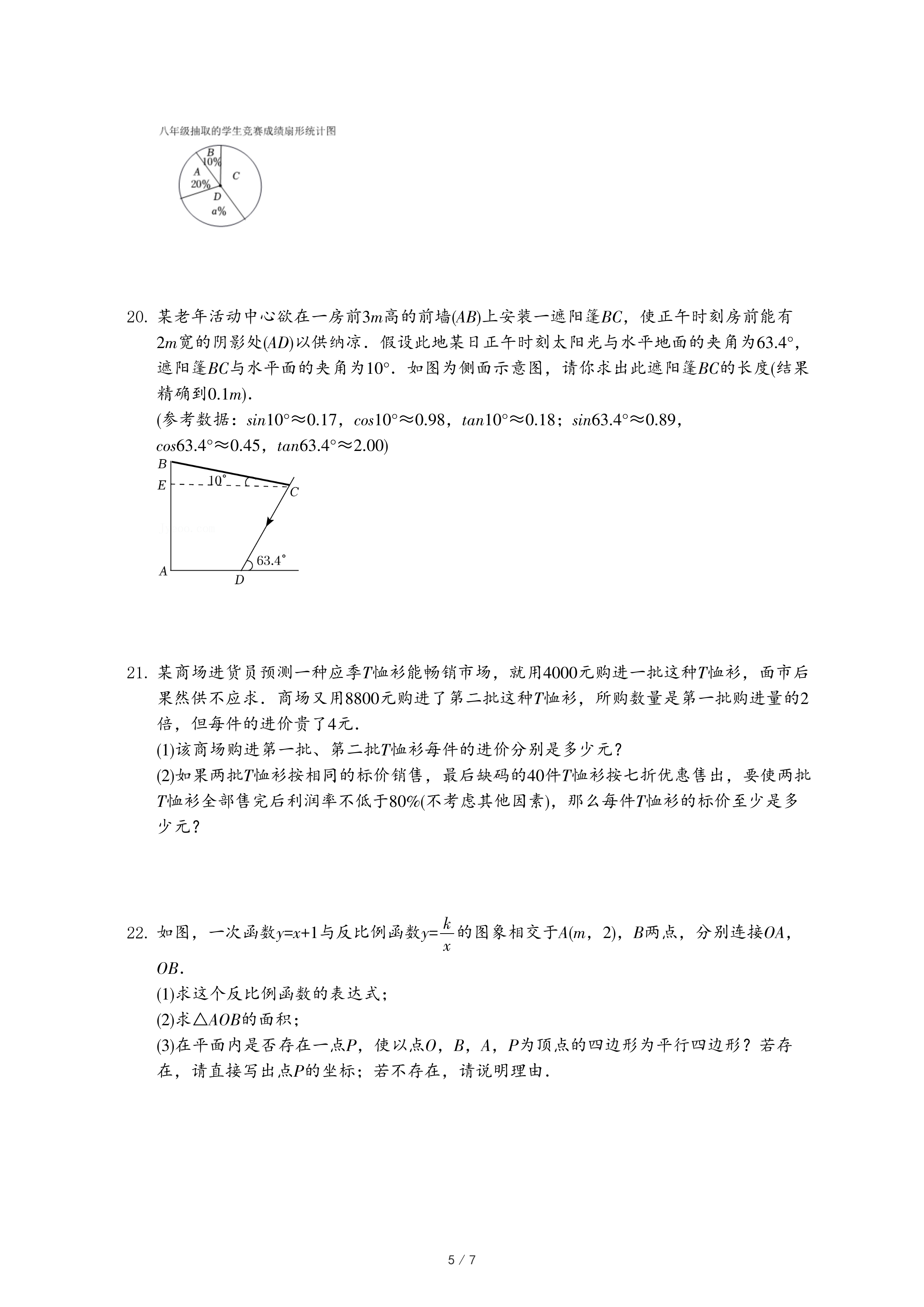
19.“防溺水”是校园安全教育工作的重点之一.某校为确保学生安全,开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:
七年级10名学生的竞赛成绩是:96,84,97,85,96,96,96,84,90,96.
八年级10名学生的竞赛成绩在C组中的数据是:92,92,94,94.
七、八年级抽取的学生竞赛成绩统计表
| 年级 | 七年级 | 八年级 |
| 平均数 | 92 | 92 |
| 中位数 | 96 | m |
| 众数 | b | 98 |
| 方差 | 28.6 | 28 |
根据以上信息,解答下列问题:
(1)上述图表中a=
,b=
,m=
;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共1200人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≥95)的学生人数是多少?