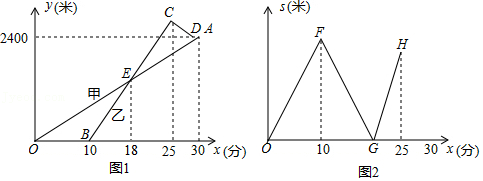
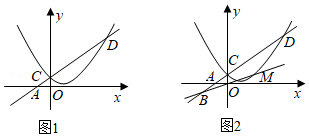
22.某校的甲、乙两位老师同住一小区,该小区与学校相距2400米.甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校又骑行若干米到达还车点后,立即步行走回学校.已知甲步行的速度比乙步行的速度每分钟快5米.设甲步行的时间为x(分),图1中线段OA和折线B-C-D分别表示甲、乙离开小区的路程y(米)与甲步行时间x(分)的函数关系的图象;图2表示甲、乙两人之间的距离s(米)与甲步行时间x(分)的函数关系的图象(不完整).
根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当25≤x≤30时s关于x的函数的大致图象.(温馨提示:请画在答题卷相对应的图上)