


| 1 |
| x-3 |



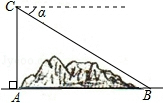
| 1000 |
| tanα |
| 1000 |
| sinα |
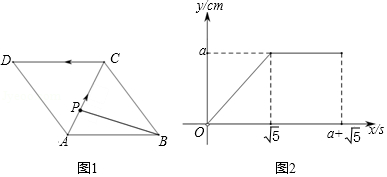
| 5 |
| 2 |
| - |
| x |
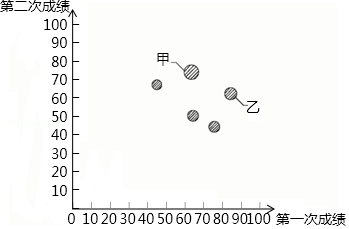
| 甲 | 乙 | 丙 | 丁 | |||
| 7 | 8 | 8 | 7 | ||
| s2 | 1 | 1.2 | 0.9 | 1.8 |

| 1 |
| 2 |
| 2x-1 |
| 3 |
| 5x+1 |
| 2 |
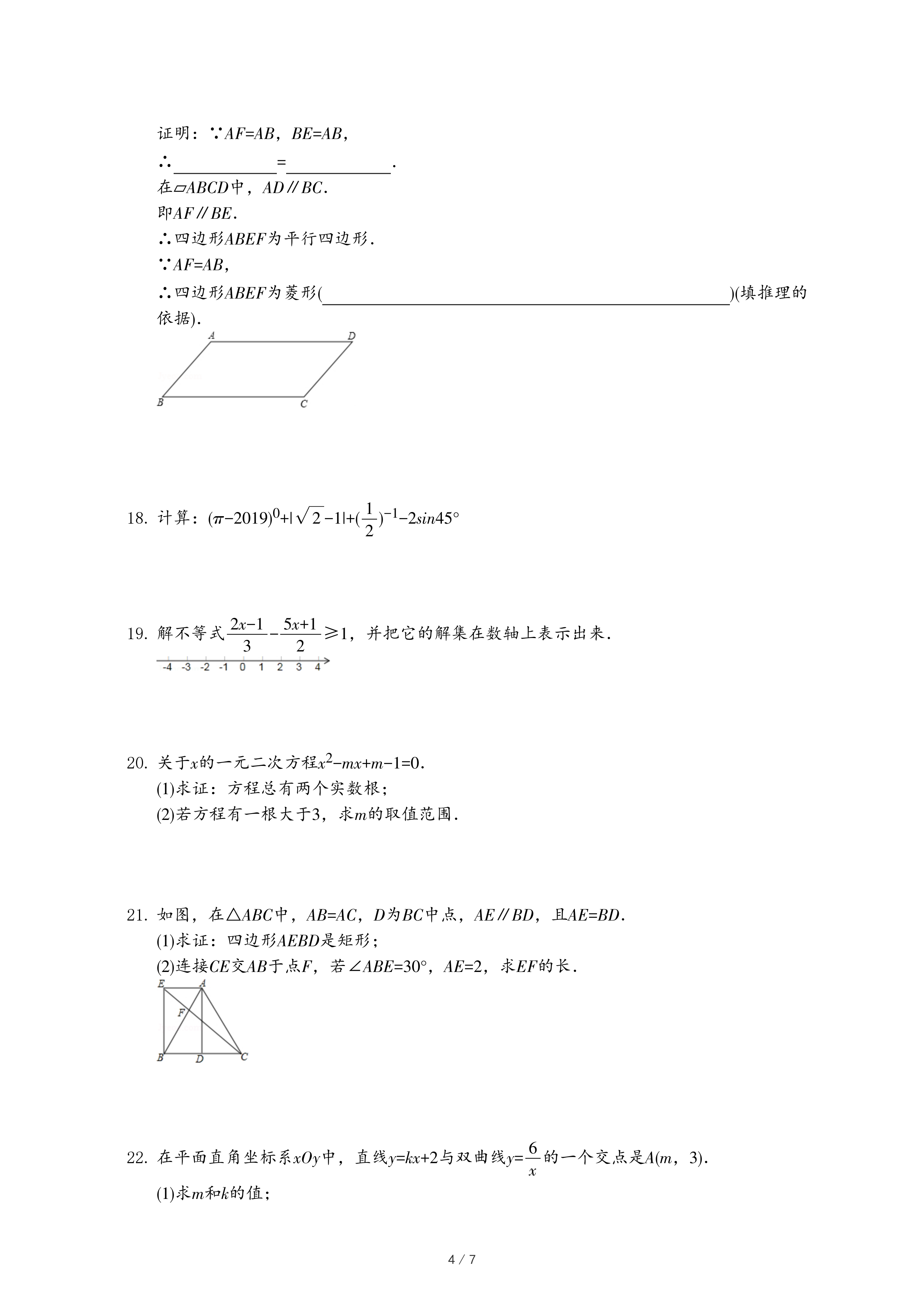
| 6 |
| x |
| 6 |
| x |
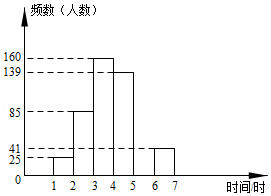
| 时间t(时) | 频数(人数) | 频率 |
| 1≤t<2 | 25 | 0.050 |
| 2≤t<3 | 85 | a |
| 3≤t<4 | 160 | 0.320 |
| 4≤t<5 | 139 | 0.278 |
| 5≤t<6 | b | 0.100 |
| 6≤t≤7 | 41 | 0.082 |
| 合计 | c | 1.000 |
| 3 |
| 5 |
| 5 √2 |
| 2 |
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 0 | 4.47 | 7.07 | 9.00 | 8.94 | 0 |