


| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 甲 | 乙 | 丙 | 丁 | |
| 平均数x(分) | 96 | 93 | 95 | 96 |
| 方差s2 | 1.2 | 0.6 | 0.6 | 0.4 |
| 1 |
| 3600 |
| 1 |
| 3600 |

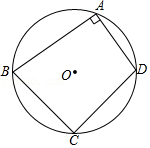
| 5 |
| 2 |
| 5 √2 |
| 2 |
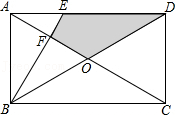
| 15 √3 |
| 4 |
| 9 √3 |
| 4 |
| 15 √3 |
| 2 |
| 9 √3 |
| 2 |
| k |
| x |
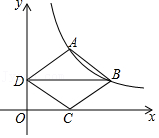
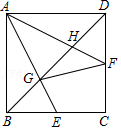
| 2 |
| 3 |
| x |
| x-2 |
| 3 |
| 2-x |
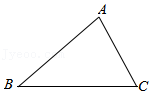
| 应聘者 | 专业知识 | 创新能力 | 语言表达 |
| 甲 | 96 | 92 | 85 |
| 乙 | 93 | 88 | 95 |
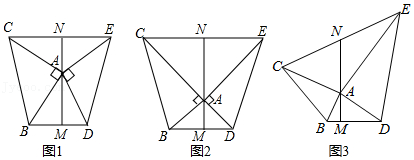
卢卡斯数列法国数学家爱德华•卢卡斯以研究斐波那契数列而著名,他曾给出了求斐波那契数列第n项的表达式,创造出了检验素数的方法,还发明了汉诺塔问题.“卢卡斯数列”是以卢卡斯命名的一个整数数列,在股市中有广泛的应用.卢卡斯数列中的第n个数F(n)可以表示为(
|

| 课题 | 测量毛主席塑像的高度组长:XXX组员:XXX,XXX,XXX测倾器,皮尺等 | |||
| 成员 | ||||
| 测量工具 | ||||
| 测量示意图 | 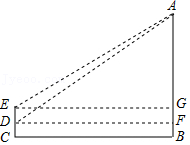 | 说明:线段AB的长表示塑像从最高点到地面之间的距离,C为测点,线段CE,CD表示测倾器(点D在CE上),点A,B,C,D,E都在同一竖直平面内,且AB⊥BC,CE⊥BC;∠ADF、∠AEG表示两次测量的仰角,点G,F在AB上. | ||
| 测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
| ∠ADF的度数 | 35.1° | 34.9° | 35.0° | |
| ∠AEG的度数 | 33.4° | 33.6° | 33.5° | |
| 测倾器CE的高 | 1.68m | 1.72m | 1.70m | |
| 测倾器CD的高 | 1.07m | 1.05m | 1.06m | |

| AB |
| AC |
| AD |
| AE |
| 1 |
| 2 |
| AB |
| AC |
| AD |
| AE |