25.中国新闻出版研究院组织实施的全国国民阅读调查已持续开展了18次,对我国国民阅读总体情况进行了综合分析.2021年4月23日,第十八次全国国民阅读调查结果发布.
下面是关于样本及国民图书阅读量的部分统计信息:
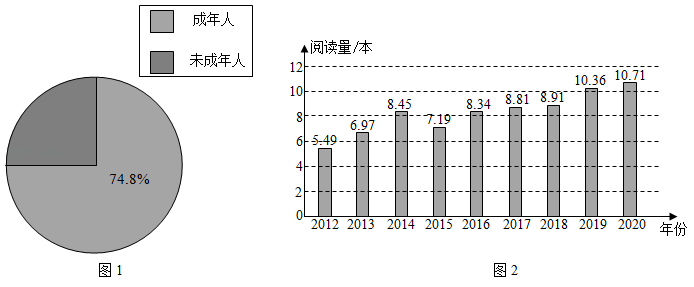
a.本次调查有效样本容量为46083,成年人和未成年人样本容量的占比情况如图1.
b.2020年,成年人的人均纸质图书阅读量约为4.70本,人均电子书阅读量约为3.29本;2019年,成年人的人均纸质图书阅读量约为4.65本,人均电子书阅读量约为2.84本.
c.2012年至2020年,未成年人的年人均图书阅读量如图2.
根据以上信息,回答问题:
(1)第十八次全国国民阅读调查中,未成年人样本容量占有效样本容量的
;
(2)2020年,成年人的人均图书阅读量约为
本,比2019年多
本;
(3)在2012年至2020年中后一年与前一年相比,
至
的增长率最大;
(4)2020年,未成年人的人均图书阅读量比成年人的人均图书阅读量高
%(结果保留整数).