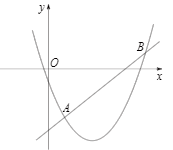
24.如图,在平面直角坐标系中,O为坐标原点,正方形ABCO的边OA落在x轴上,OC落在y轴上,OA=OC=2,已知直线l:y=x+k.
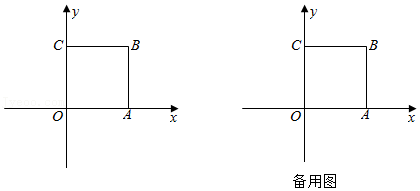
(1)填空:B(
,
),当直线l与正方形ABCO没有交点时,k的取值范围是:
;
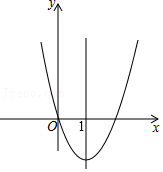
(2)当k=0时,已知抛物线L:y=a(x-m)
2+n(a<0)顶点P在直线l上,设抛物线与直线l的另一个交点为M,过M作MN∥x轴交抛物线于另一点N,若MN=2,求a的值;
(3)在(2)的条件下,抛物线L与边AB所在的直线交于点E.
①当点P向上运动的过程中,点E也随之向上运动,求此时m的取值范围,并写出点E在最高位置时的坐标;
②若抛物线L与线段OA只有一个公共点,求m的取值范围.