17．计算：2cos30°-()^-2+(π-2)⁰-．

18．解不等式组：．

19．已知m²+m-3=0，求代数式(m+)÷的值．

20．已知：如图，点M为锐角∠APB的边PA上一点．
求作：∠AMD，使得点D在边PB上，且∠AMD=2∠P．
作法：①以点M为圆心，MP长为半径画圆，交PA于另一点C，交PB于点D；
②作射线MD．
(1)使用直尺和圆规，依作法补全图形(保留作图痕迹)；
(2)完成下面的证明．
证明：∵P、C、D都在⊙M上，
∠P为⌒CD所对的圆周角，∠CMD为⌒CD所对的圆心角，
∴∠P=∠CMD(      )(填推理依据)．
∴∠AMD=2∠P．

21．如图，一个单向隧道的断面，隧道顶是一条抛物线的一部分，经测量，隧道顶的跨度为4米，最高处到地面的距离为4米，两侧墙高均为3米，距左侧墙壁1米和3米时，隧道高度均为3.75米．设距左侧墙壁水平距离为x米的地点，隧道高度为y米．
请解决以下问题：
(1))在下边网格中建立适当的平面直角坐标系，根据题中数据描点，并用平滑的曲线连接；
(2)请结合所画图象，写出抛物线的对称轴；
(3)今有宽为2.4米的卡车在隧道中间行驶，如果卡车载物后的高度为3.2米，要求卡车从隧道中间通过时，为保证安全，要求卡车载物后最高点到隧道顶面对应的点的距离均不小于0.6米，结合所画图象，试判断该卡车能否通过隧道．

22．如图，在▱ABCD中，过点B作BE⊥CD交CD的延长线于点E，过点C作CF∥EB交AB的延长线于点F．
(1)求证：四边形BFCE是矩形；
(2)连接AC，若AB=BE=2，tan∠FBC=，求AC的长．

23．一次函数y=kx+4k(k≠0)的图象与x轴交于点A，与y轴交于点B，且经过点C(2，m)．
(1)当m=时，求一次函数的解析式并求出点A的坐标；
(2)当x＞-1时，对于x的每一个值，函数y=x的值大于一次函数y=kx+4k(k≠0)的值，求k的取值范围．

24．如图，BE是⊙O直径，点A是⊙O外一点，OA⊥OB，AP切⊙O于点P，连接BP交AO于点C．
(1)求证：∠PAO=2∠PBO；
(2)若⊙O的半径为5，tan∠PAO=，求BP的长．

25．为庆祝中国共产党建党100周年，讴歌中华民族实现伟大复兴的奋斗历程，继承革命先烈的优良传统，某中学开展了建党100周年知识测试．该校七、八年级各有300名学生参加，从中各随机抽取了50名学生的成绩(百分制)，并对数据(成绩)进行整理，描述和分析，下面给出了部分信息：
a．八年级的频数分布直方图如下(数据分为5组：50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100)；
b．八年级学生成绩在80≤x＜90的这一组是：
80  81  82  83  83  83.583.5  84  84  85  86  86.5  87  88  89  89
七、八年级学生成绩的平均数、中位数、众数如表：
根据以上信息，回答下列问题：
(1)表中m的值为       ；
(2)在随机抽样的学生中，建党知识成绩为84分的学生，在       年级抽样学生中排名更靠前，理由是       ；
(3)若成绩85分及以上为“优秀”，请估计八年级达到“优秀”的人数．

26．已知二次函数y=x²+bx+c(b，c为常数)的图象经过点A(1，0)与点C(0，-3)，其顶点为P．
(1)求二次函数的解析式及P点坐标；
(2)当m≤x≤m+1时，y的取值范围是-4≤y≤2m，求m的值．

27．已知：等边△ABC，过点B作AC的平行线l．点P为射线AB上一个动点(不与点A，B重合)，将射线PC绕点P顺时针旋转60°交直线l于点D．
(1)如图1，点P在线段AB上时，依题意补全图形；
①求证：∠BDP=∠PCB；
②用等式表示线段BC，BD，BP之间的数量关系，并证明；
(2)点P在线段AB的延长线上，直接写出线段BC，BD，BP之间的数量关系．

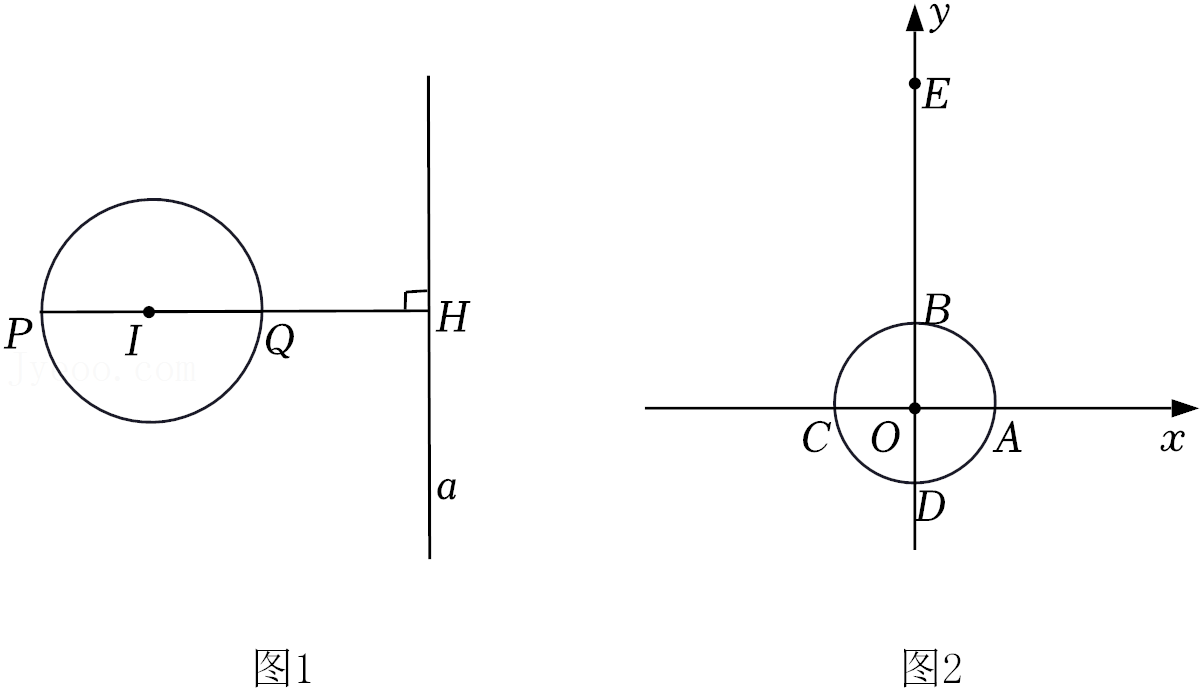
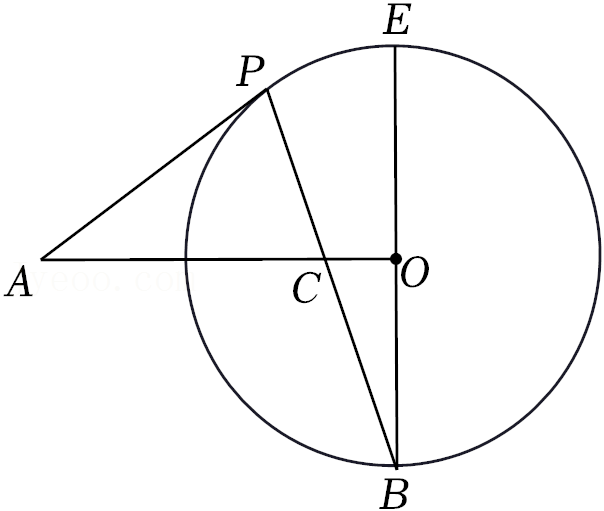
28．如图1，⊙I与直线a相离，过圆心I作直线a的垂线，垂足为H，且交⊙I于P，Q两点(Q在P，H之间)我们把点P称为⊙I关于直线a的“远点”，把PQ•PH的值称为⊙I关于直线a的“特征数”．
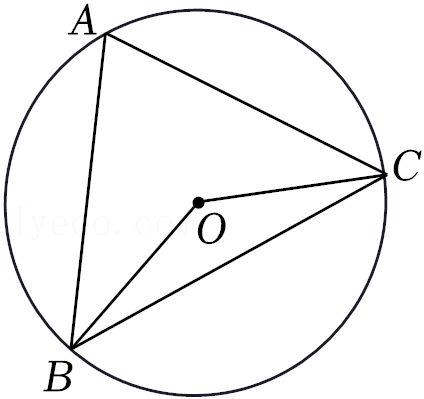
(1)如图2，在平面直角坐标系xOy中，点E的坐标为(0，4)，半径为1的⊙O与两坐标轴交于点A，B，C，D．
①过点E作垂直于y轴的直线m，则⊙O关于直线m的“远点”是点       (填“A”，“B”，“C”或“D”)，⊙O关于直线m的“特征数”为       ；
②若直线n的函数表达式为y=x+4，求⊙O关于直线n的“特征数”；
(2)在平面直角坐标系xOy中，直线l经过点M(1，4)，点F是坐标平面内一点，以F为圆心，为半径作⊙F．若⊙F与直线l相离，点N(-1，0)是⊙F关于直线l的“远点”，且⊙F关于直线l的“特征数”是6，直接写出直线l的函数解析式．