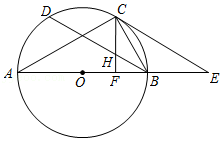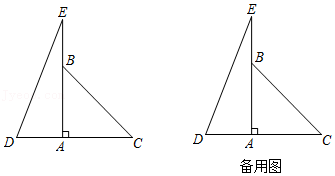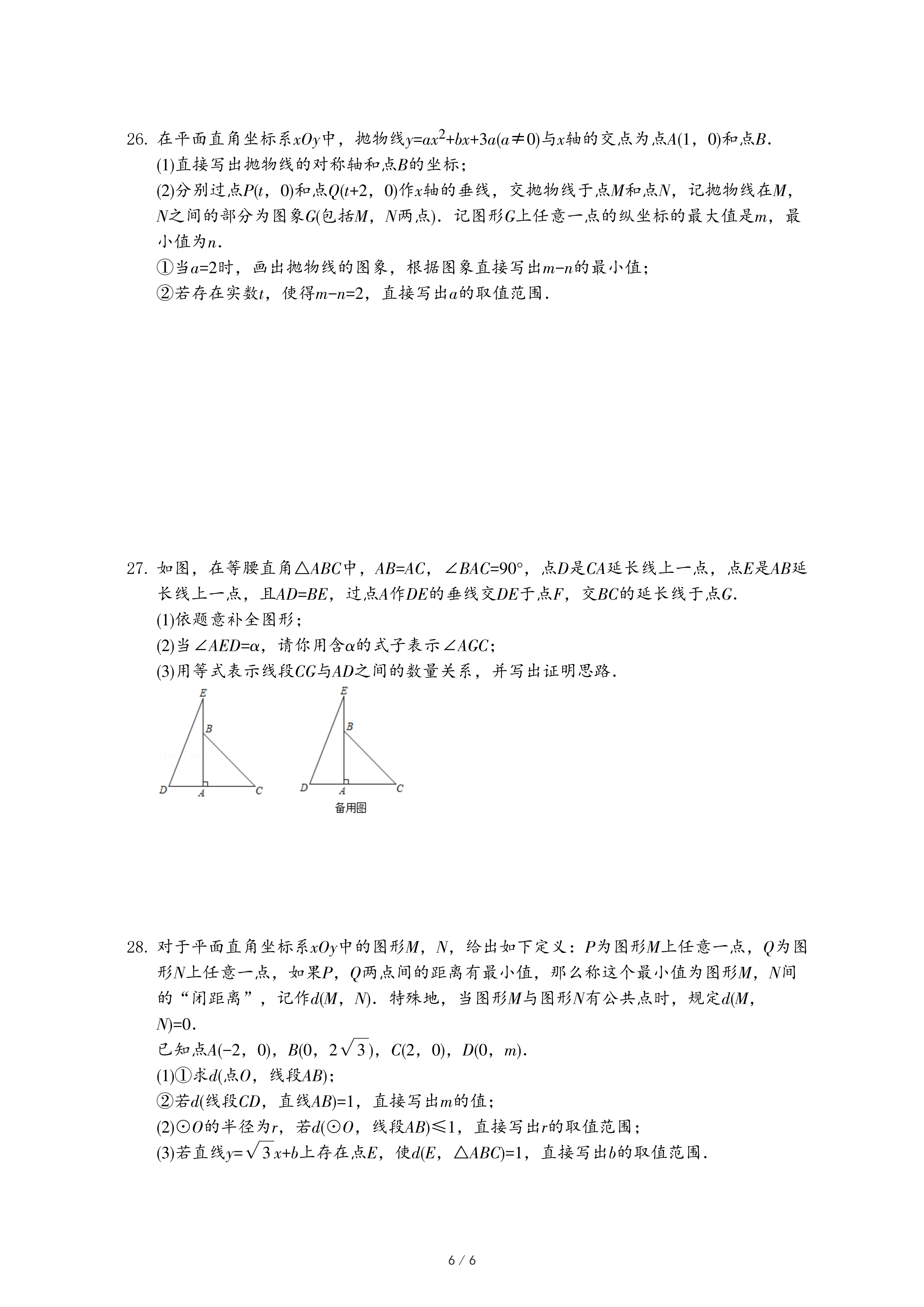



 等边三角形
等边三角形 圆
圆 正方形
正方形 正六边形
正六边形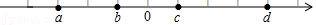
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 摄氏(单位℃) | … | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 华氏(单位℉) | … | 32 | 33.8 | 35.6 | 37.4 | 39.2 | 41 | 42.8 | … |
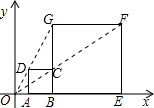
| 1班 | 65 | 70 | 70 | 70 | 75 | 82 |
| 2班 | 55 | 70 | 70 | 75 | 80 | 82 |
| 1 |
| 2 |
| 1 |
| 2 |
| 成绩x学校 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
| 甲 | 4 | 15 | 9 | 10 | 2 |
| 乙 | 6 | 3 | 15 | 14 | 2 |
| 学校 | 平均分 | 中位数 | 众数 |
| 甲 | 74.2 | n | 85 |
| 乙 | 73.5 | 76 | 84 |
| k |
| x |