


 厨余垃圾FoodWaste
厨余垃圾FoodWaste 可回收物Recyclable
可回收物Recyclable 其他垃圾ResidualWaste
其他垃圾ResidualWaste 有害垃圾HazardousWaste
有害垃圾HazardousWaste


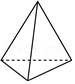

| 1 |
| y |
| 1 |
| x |
| xy |
| x2-y2 |
| 1 |
| 2 |
| 1 |
| 2 |





| 加工方式 | 加工成本 | 销售单位 | 售价 |
| 直接卖 | 0 | 个 | 2元/个 |
| 粗加工 | 1元/个 | 包装袋(一袋5个) | 30元/袋 |
| 精加工 | 2.5元/个 | 礼盒(一盒10个) | 85元/盒 |
| 1 |
| 2 |

| 3 |
| 4 |

| k |
| x |

| 节数x | 频数 | 频率 |
| 0≤x<10 | 8 | 0.16 |
| 10≤x<20 | 10 | 0.20 |
| 20≤x<30 | 16 | b |
| 30≤x<40 | a | 0.24 |
| x≥40 | 4 | 0.08 |
| 总数 | 50 | 1 |


| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y1/cm | 5.24 | 4.24 | 3.24 | 1.54 | 1.79 | 3.47 | |
| y2/cm | 1.31 | 1.34 | 1.42 | 1.54 | 1.80 | 2.45 | 3.47 |


