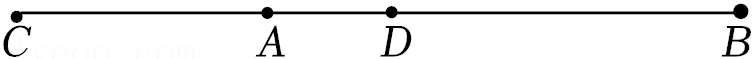27.阅读材料并回答问题:
数学课上,老师提出了如下问题:
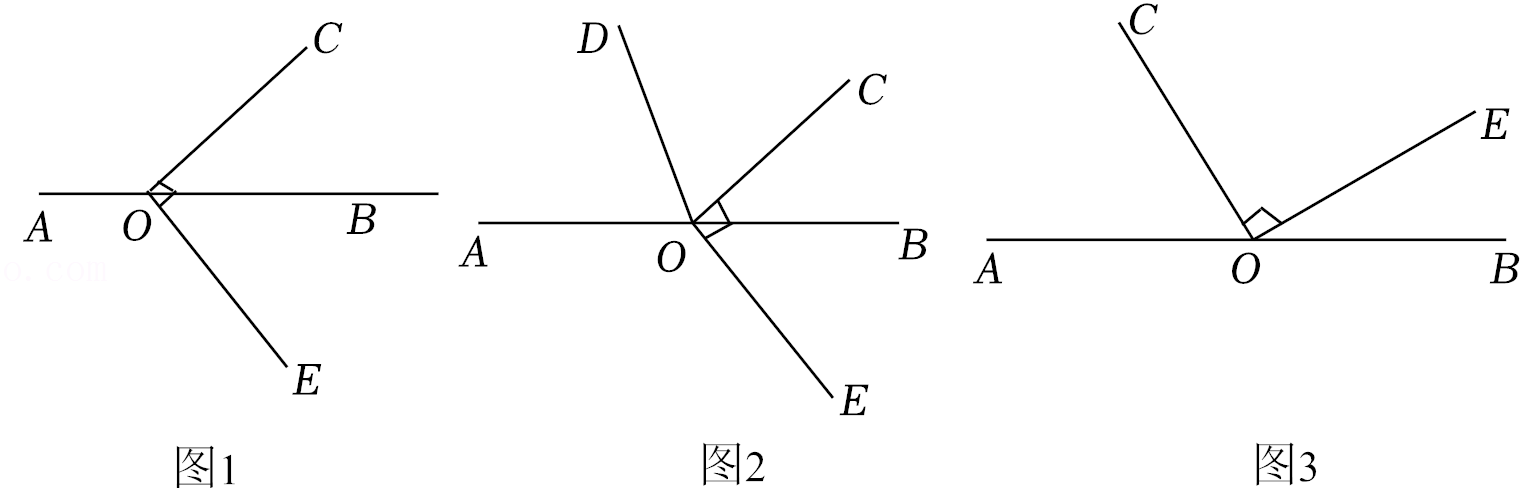
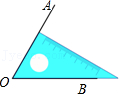
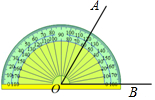
已知点O在直线AB上,∠COE=90°,在同一平面内,过点O作射线OD,满足∠AOC=2∠AOD.当∠BOC=40°时,如图1所示,求∠DOE的度数.
甲同学:以下是我的解答过程(部分空缺)
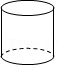
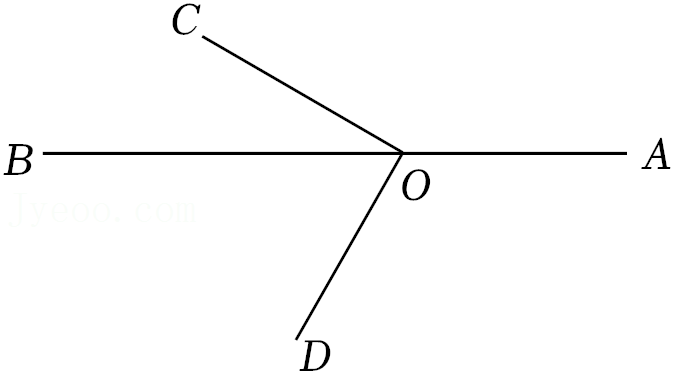
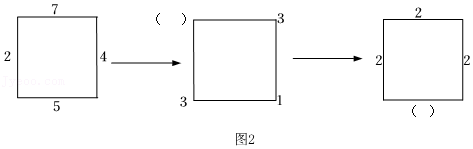
解:如图2,∵点O在直线AB上,
∴∠AOB=180°.
∵∠BOC=40°,
∴∠AOC=________°.
∵∠AOC=2∠AOD,
∴OD平分∠AOC.
∴∠COD=
∠AOC=________°.
∵∠DOE=∠COD+∠COE,∠COE=90°,
∴∠DOE=________°.
乙同学:“我认为还有一种情况.”
请完成以下问题:
(1)请将甲同学解答过程中空缺的部分补充完整.
(2)判断乙同学的说法是否正确,若正确,请在图1中画出另一种情况对应的图形,并求∠DOE的度数,写出解答过程;若不正确,请说明理由.
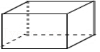
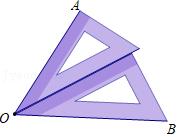
(3)将题目中“∠BOC=40°”的条件改成“∠BOC=α”,其余条件不变,当α在90°到180°之间变化时,如图3所示,α为何值时,∠COD=∠BOE成立?请直接写出此时α的值.