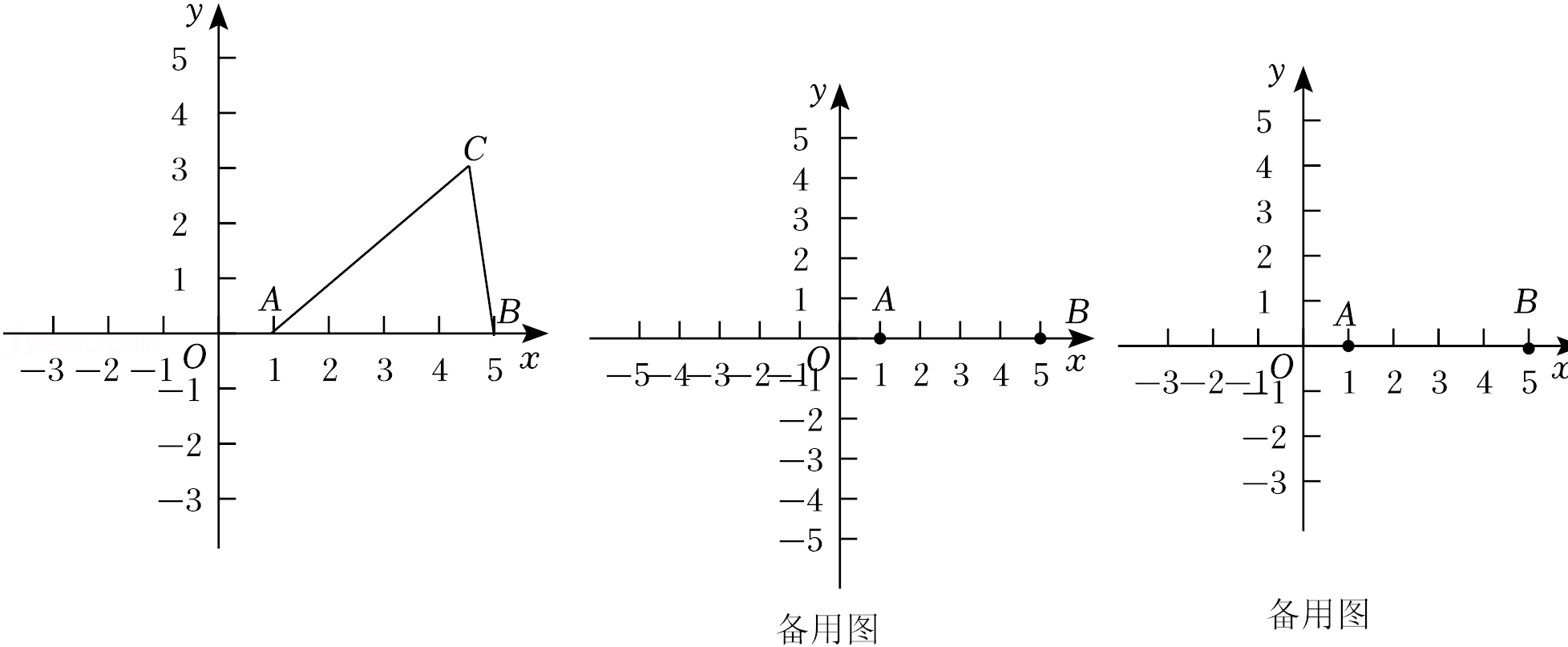
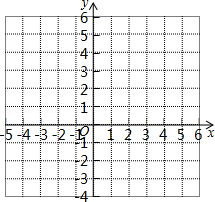28.在平面直角坐标系xOy中,已知点A(1,0)和点B(5,0).对于线段AB和直线AB外的一点C,给出如下定义:点C到线段AB两个端点的连线所构成的夹角∠ACB叫做线段AB关于点C的可视角,其中点C叫做线段AB的可视点.
(1)在点D(-2,2)、E(1,4)、F(3,-2)中,使得线段AB的可视角为45°的可视点是
;
(2)⊙P为经过A,B两点的圆,点M是⊙P上线段AB的一个可视点.
①当AB为⊙P的直径时,线段AB的可视角∠AMB为
度;
②当⊙P的半径为4时,线段AB的可视角∠AMB为
度;
(3)已知点N为y轴上的一个动点,当线段AB的可视角∠ANB最大时,求点N的坐标.