17．解方程：x²-2x-2=0．

18．问题：如图，AB是⊙O的直径，点C在⊙O内，请仅用无刻度的直尺，作出△ABC中AB边上的高．
小芸解决这个问题时，结合圆以及三角形高线的相关知识，设计了如下作图过程．
作法：如图，
①延长AC交⊙O于点D，延长BC交⊙O于点E；
②分别连接AE，BD并延长相交于点F；
③连接FC并延长交AB于点H．
所以线段CH即为△ABC中AB边上的高．
(1)根据小芸的作法，补全图形；
(2)完成下面的证明．
证明：∵AB是⊙O的直径，点D，E在⊙O上，
∴∠ADB=∠AEB=      °．(       )(填推理的依据)
∴AE⊥BE，BD⊥AD．
∴AE，      是△ABC的两条高线．
∵AE，BD所在直线交于点F，
∴直线FC也是△ABC的高所在直线．
∴CH是△ABC中AB边上的高．

19．已知二次函数y=x²+4x+3．
(1)求此函数图象的对称轴和顶点坐标；
(2)画出此函数的图象；
(3)若点A(0，y₁)和B(m，y₂)都在此函数的图象上，且y₁＜y₂，结合函数图象，直接写出m的取值范围．

20．如图，在正方形ABCD中，射线AE与边CD交于点E，将射线AE绕点A顺时针旋转，与CB的延长线交于点F，BF=DE，连接FE．
(1)求证：AF=AE；
(2)若∠DAE=30°，DE=2，直接写出△AEF的面积．

21．已知关于x的一元二次方程x²-(k+5)x+6+2k=0．
(1)求证：此方程总有两个实数根；
(2)若此方程恰有一个根小于-1，求k的取值范围．

22．有甲、乙两个不透明的口袋，甲口袋中装有两个相同的球，它们分别写有数-2，2；乙口袋中装有三个相同的球，它们分别写有数-5，m，5．小明和小刚进行摸球游戏，规则如下：先从甲口袋中随机取出一个球，其上的数记为a；再从乙口袋中随机取出一个球，其上的数记为b．若a＜b，小明胜；若a=b，为平局；若a＞b，小刚胜．
(1)若m=-2，用树状图或列表法分别求出小明、小刚获胜的概率；
(2)当m为何值时，小明和小刚获胜的概率相同？直接写出一个符合条件的整数m的值．

23．如图，AB，AC是⊙O的两条切线，切点分别为B，C，连接CO并延长交⊙O于点D，过点D作⊙O的切线交AB的延长线于点E，EF⊥AC于点F．
(1)求证：四边形CDEF是矩形；
(2)若CD=2，DE=2，求AC的长．

24．某篮球队员的一次投篮命中，篮球从出手到命中行进的轨迹可以近似看作抛物线的一部分，表示篮球距地面的高度y(单位：m)与行进的水平距离x(单位：m)之间关系的图象如图所示．已知篮球出手位置A与篮筐的水平距离为4.5m，篮筐距地面的高度为3.05m；当篮球行进的水平距离为3m时，篮球距地面的高度达到最大为3.3m．
(1)图中点B表示篮筐，其坐标为       ，篮球行进的最高点C的坐标为       ；
(2)求篮球出手时距地面的高度．

25．如图，AB是⊙O的直径，四边形ABCD内接于⊙O，D是⌒AC的中点，DE⊥BC交BC的延长线于点E．
(1)求证：DE是⊙O的切线；
(2)若AB=10，BC=8，求BD的长．

26．在平面直角坐标系xOy中，抛物线y=a(x-h)²-8a的顶点为A，0＜h＜．
(1)若a=1，
①点A到x轴的距离为       ；
②求此抛物线与x轴的两个交点之间的距离；
(2)已知点A到x轴的距离为4，此抛物线与直线y=-2x+1的两个交点分别为B(x₁，y₁)，C(x₂，y₂)，其中x₁＜x₂，若点D(x_D，y_D)在此抛物线上，当x₁＜x_D＜x₂时，y_D总满足y₂＜y_D＜y₁，求a的值和h的取值范围．

27．如图1，在△ABC中，∠ACB=90°，CA=CB，点D，E分别在边CA，CB上，CD=CE，连接DE，AE，BD．点F在线段BD上，连接CF交AE于点H．
(1)①比较∠CAE与∠CBD的大小，并证明；
②若CF⊥AE，求证：AE=2CF；
(2)将图1中的△CDE绕点C逆时针旋转α(0°＜α＜90°)，如图2．若F是BD的中点，判断AE=2CF是否仍然成立．如果成立，请证明；如果不成立，请说明理由．

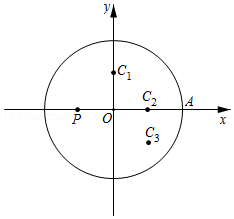
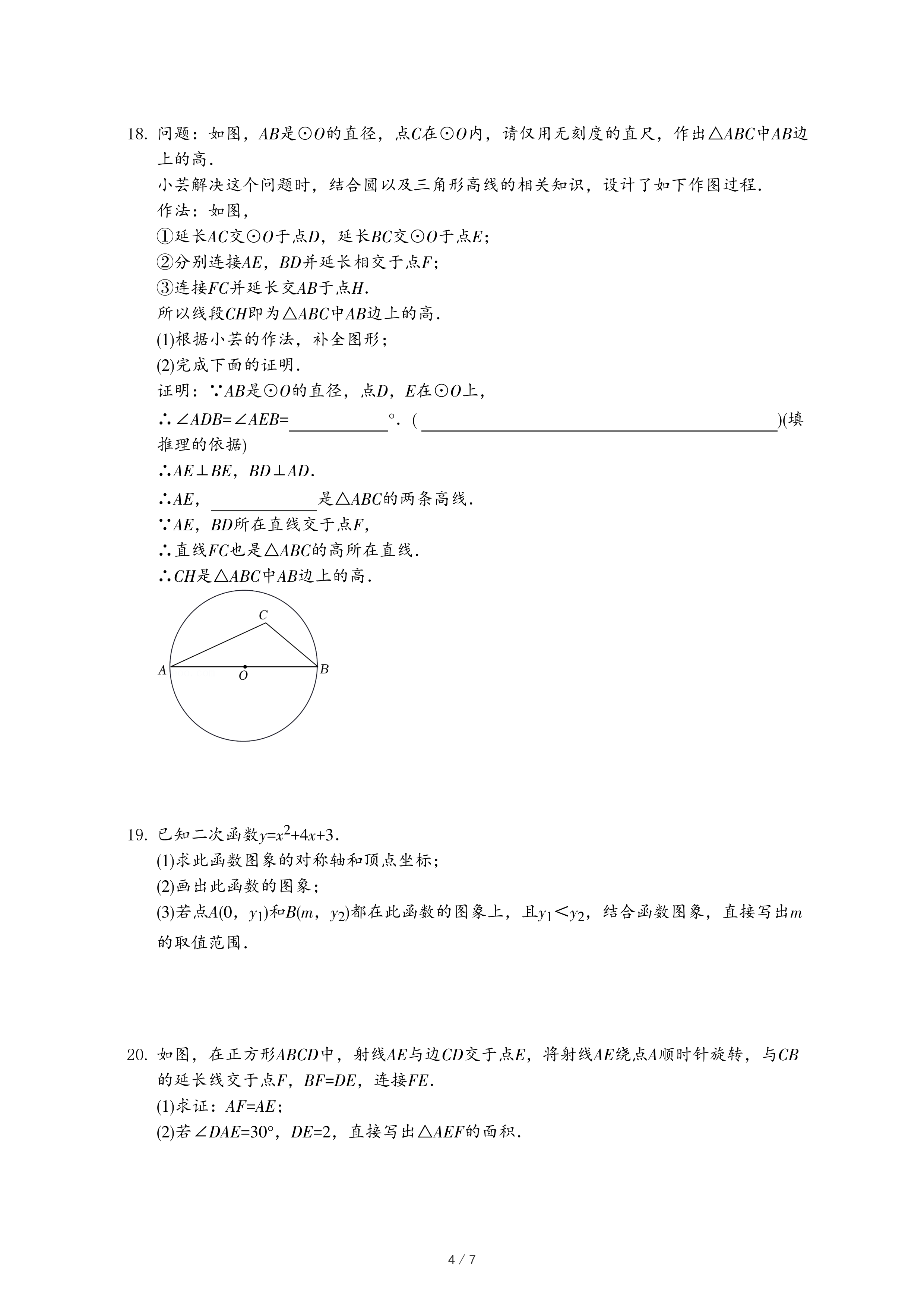
28．在平面直角坐标系xOy中，⊙O的半径为1，点A在⊙O上，点P在⊙O内，给出如下定义：连接AP并延长交⊙O于点B，若AP=kAB，则称点P是点A关于⊙O的k倍特征点．
(1)如图，点A的坐标为(1，0)．
①若点P的坐标为(-，0)，则点P是点A关于⊙O的     倍特征点；
②在C₁(0，)，C₂(，0)，C₃(，-)这三个点中，点       是点A关于⊙O的倍特征点；
③直线l经过点A，与y轴交于点D，∠DAO=60°．点E在直线l上，且点E是点A关于⊙O的倍特征点，求点E的坐标；
(2)若当k取某个值时，对于函数y=-x+1(0＜x＜1)的图象上任意一点M，在⊙O上都存在点N，使得点M是点N关于⊙O的k倍特征点，直接写出k的最大值和最小值．