












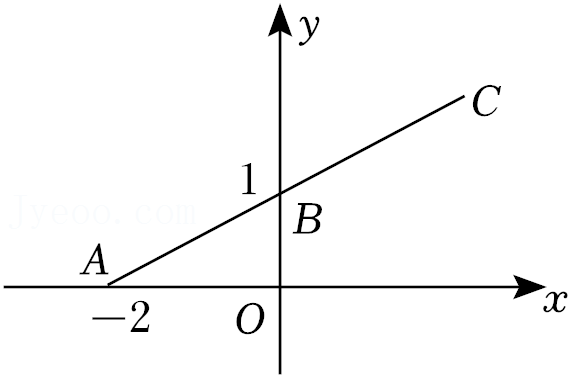
| 1 |
| x |
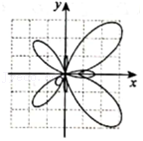
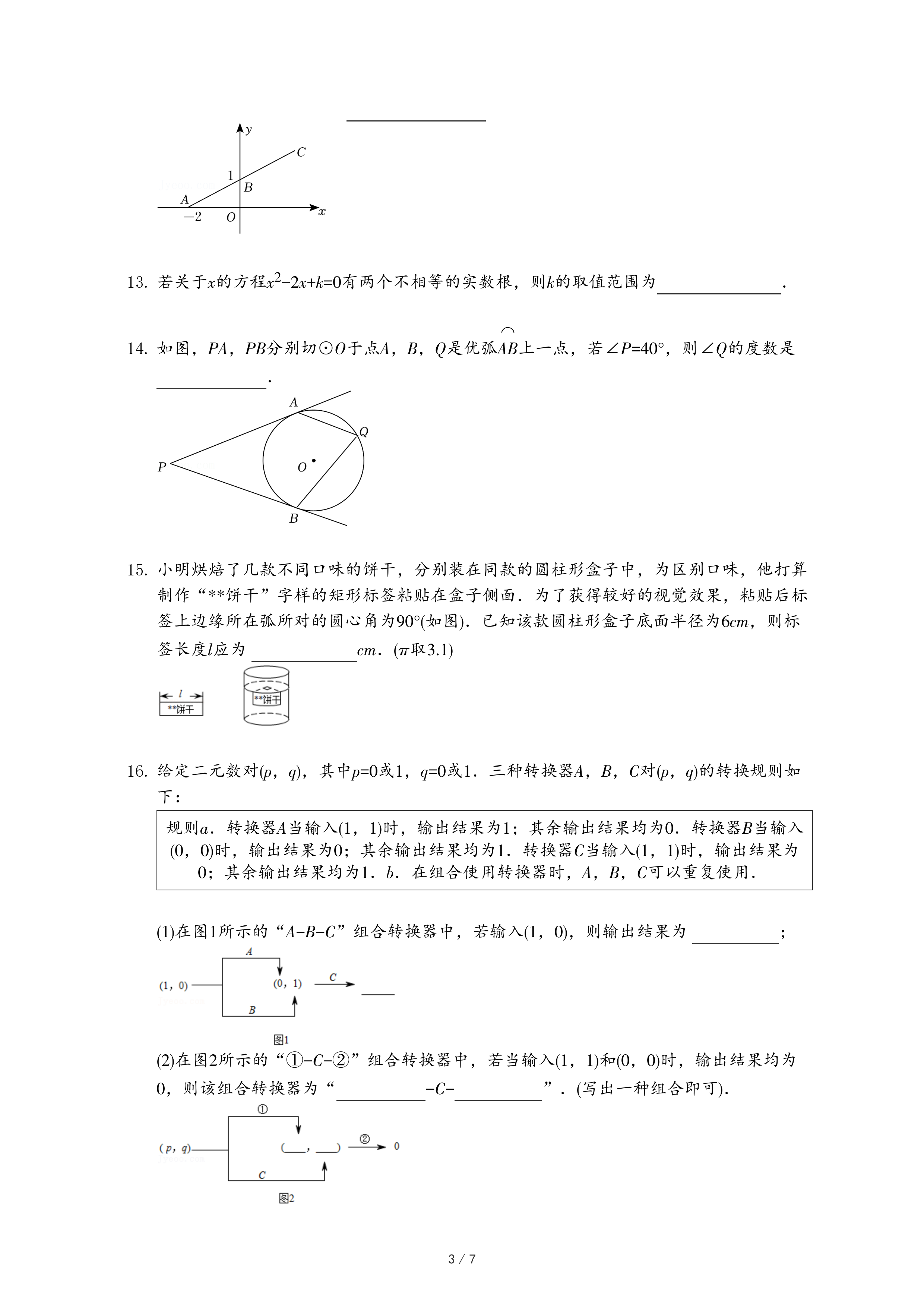
 绕某点连续旋转若干次,每次旋转相同角度α,设计出一个外轮廓为正六边形的图案(如图),则α可以为( )
绕某点连续旋转若干次,每次旋转相同角度α,设计出一个外轮廓为正六边形的图案(如图),则α可以为( )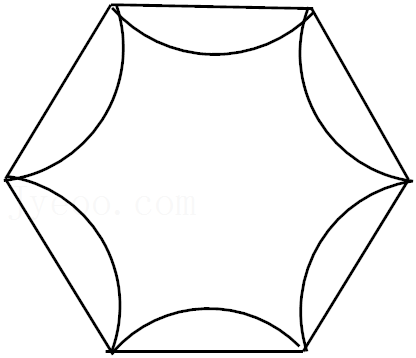
| 抛掷次数m | 500 | 1000 | 1500 | 2000 | 2500 | 3000 | 4000 | 5000 | ||
| “正面向上”的次数n | 265 | 512 | 793 | 1034 | 1306 | 1558 | 2083 | 2598 | ||
“正面向上”的频率
| 0.530 | 0.512 | 0.529 | 0.517 | 0.522 | 0.519 | 0.521 | 0.520 |
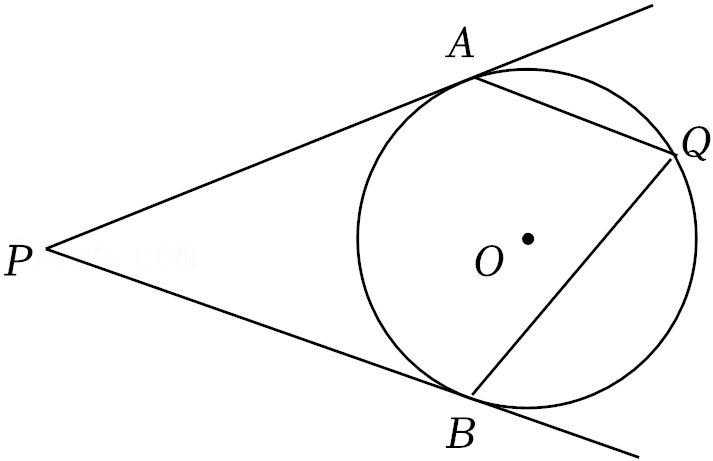
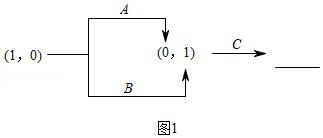
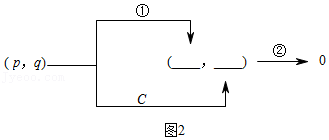
| 规则a.转换器A当输入(1,1)时,输出结果为1;其余输出结果均为0.转换器B当输入(0,0)时,输出结果为0;其余输出结果均为1.转换器C当输入(1,1)时,输出结果为0;其余输出结果均为1.b.在组合使用转换器时,A,B,C可以重复使用. |
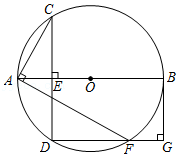
| 1 |
| 2 |