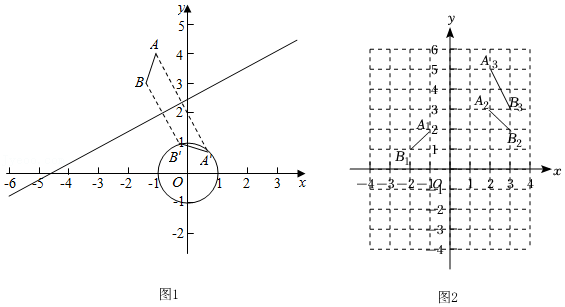
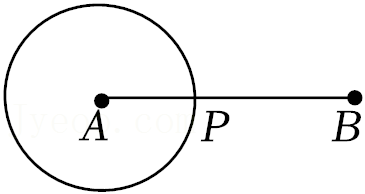
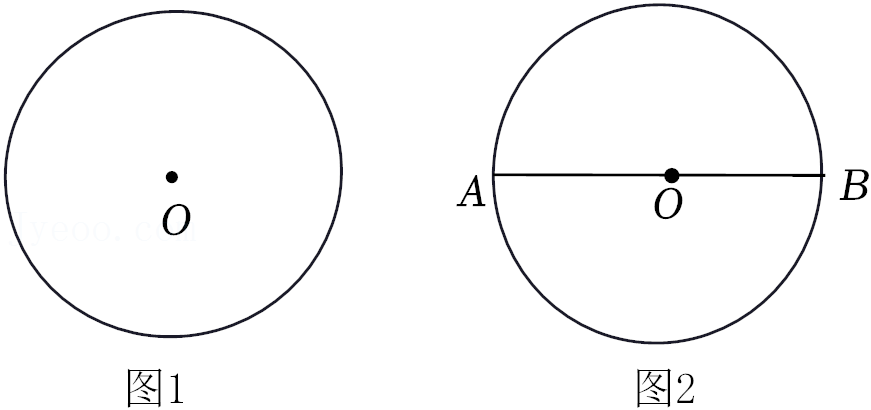
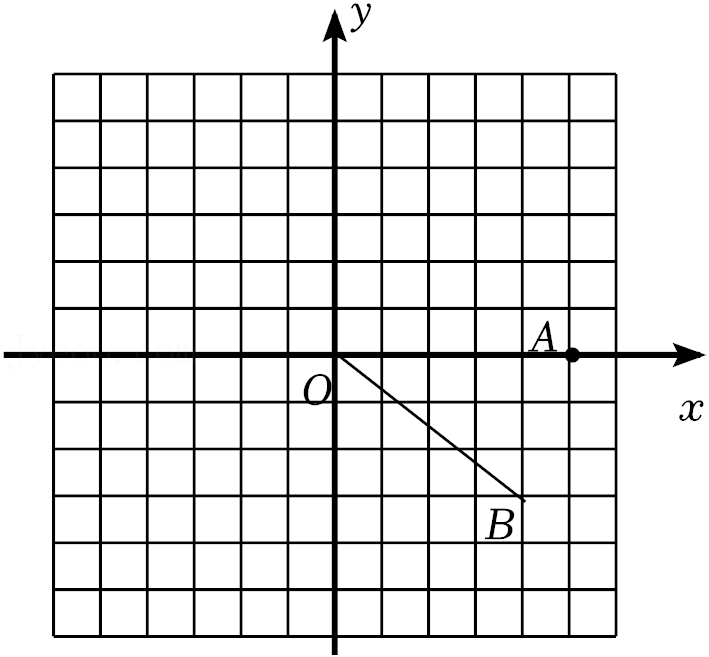
28.在平面直角坐标系xOy中.⊙O的半径为1,对于直线l和线段AB,给出如下定义:若将线段AB关于直线l对称,可以得到⊙O的弦A′B′(A′,B′分别为A,B的对应点),则称线段AB是⊙O的关于直线l对称的“关联线段”.例如:在图1中,线段AB是⊙O的关于直线l对称的“关联线段”.
(1)如图2,点A
1,B
1,A
2,B
2,A
3,B
3的横、纵坐标都是整数.
①在线段A
1B
1,A
2B
2,A
3B
3中,⊙O的关于直线y=x+2对称的“关联线段”是
;
②若线段A
1B
1,A
2B
2,A
3B
3中,存在⊙O的关于直线y=-x+m对称的“关联线段”,则m=
;
(2)已知直线y=-
x+b(b>0)交x轴于点C,在△ABC中,AC=3,AB=1.若线段AB是⊙O的关于直线y=-
x+b(b>0)对称的“关联线段”,直接写出b的最大值和最小值,以及相应的BC长.