












| 1 |
| 2 |
| 1 |
| 2 |




| x2 |
| x-1 |
| 1 |
| 1-x |
| 1 |
| x+1 |
| x |
| x-1 |
| 900 |
| x+1 |
| 900 |
| x-3 |
| 900 |
| x+1 |
| 900 |
| x-3 |
| 900 |
| x-1 |
| 900 |
| x+3 |
| 900 |
| x-1 |
| 900 |
| x+3 |
| 12 |
| 13 |
| 5 |
| 13 |
| 12 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |


| GC |
| BG |
| 1 |
| 2 |
| 4 √5 |
| 3 |
| 9 |
| 2 |
| 3 √5 |
| 2 |

| k |
| x |
| AE |
| CE |
| 2 |
| 3 |
| k |
| x |
| CE |
| BE |




| 草莓等级 | 每包中草莓重量(千克) | 售价(元/包) | 每个包装盒的成本(元) |
| A级 | 1 | 80 | 2 |
| B级 | 2 | 120 | 2 |
| DE |
| EC |
| 1 |
| 2 |
| AE |
| BE |
| 1 |
| 2 |
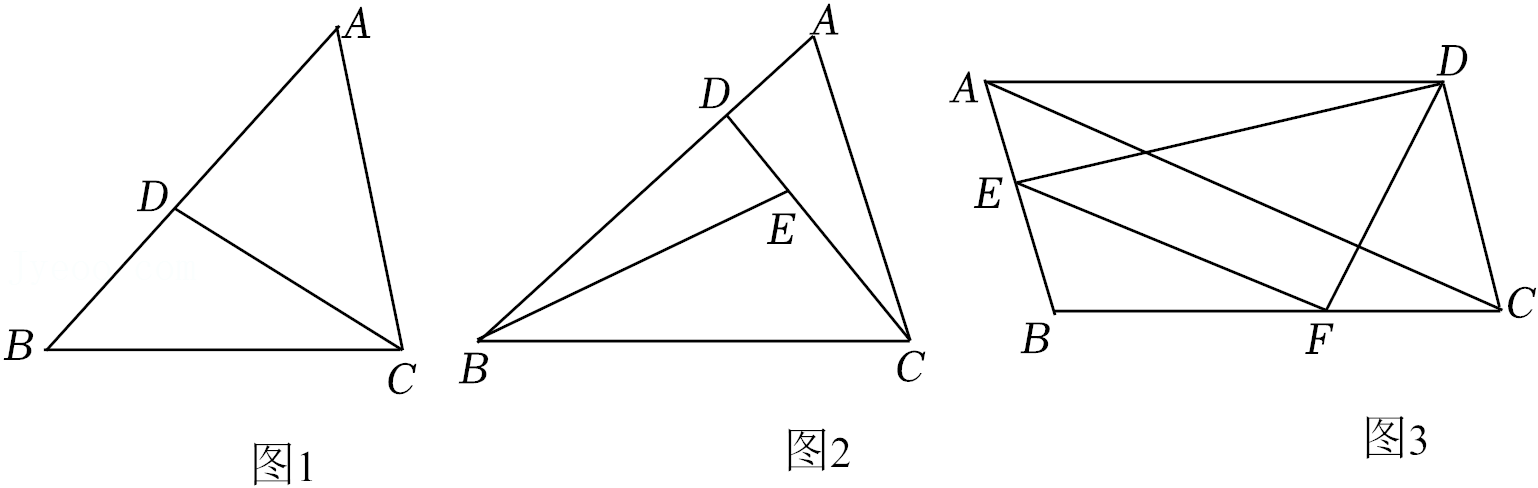
| FC |
| EC |
