


| 区县 | 大兴 | 通州 | 平谷 | 顺义 | 怀柔 | 门头沟 | 延庆 | 昌平 | 密云 | 房山 |
| 最高气温 | 32 | 32 | 30 | 32 | 30 | 32 | 29 | 32 | 30 | 32 |
| 4 |
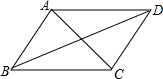
| 3 |
| x(℃) | 0 | 5 | 10 | 15 | 20 | 25 |
| y(m/s) | 331 | 334 | 337 | 340 | 343 | 346 |
| 教学能力 | 科研能力 | 组织能力 | |
| 甲 | 81 | 85 | 86 |
| 乙 | 92 | 80 | 74 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 23 |
| 3 |
| (23-2)+2 |
| 22-1 |
| 2(22-1)+2 |
| 22-1 |
| 2 |
| 3 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 33 |
| 8 |
| (33-3)+3 |
| 32-1 |
| 3(32-1)+3 |
| 32-1 |
| 3 |
| 8 |
| 4 |
| 15 |
| 1 |
| 3 |