15．已知：∠O及其两边上的点A、B．
求作：四边形OACB，使点C在∠O内部，AC∥OB，且∠ACB=90°．

16．(1)计算：(-)÷；
(2)解不等式组：，并写出它的正整数解．

17．在践行青岛市中小学生全面发展“十个一”活动中，小明到青岛某景点进行了一次研学．该景点出售三种青岛特色景点明信片①“五月的风”②“秀美崂山”③“栈桥记忆”．小明在如图四张明信片中随机抽取了两张，请用列表或画树状图的方法，求出他抽取的组合为“五月的风+秀美崂山”的概率．

18．如图，AB、CD是建筑工地上两建筑物，建筑物CD的高度为22米，在建筑物AB顶部测得建筑物CD底部的俯角为26.6°，测得建筑物CD顶部的仰角为53°．现工人需用一根绳子将点A和点C连接(绳子不弯折)，试求绳子AC的长度．
(参考数据：sin53°≈，cos53°≈，tan53°≈，sin22.6°≈，cos26.6°≈，tan22.6°≈)

19．为响应“双减”政策，老师们都精心设计每天的作业，青岛某学校调查了该校部分学生每天完成作业所用时间，并用得到的数据绘制了如下不完整的统计图．

根据图中信息回答下列问题：
(1)本次调查属于      (选填“普查”或“抽样调查”)；
(2)本次共调查学生      人，调查学生完成作业所用时间的众数是      ；
(3)将条形统计图补充完整；
(4)估计该校学生完成作业所用的平均时间．

20．“菊润初经雨，橙香独占秋”，如图，橙子是一种甘甜爽口的水果，富含维生素C．某水果商城为了了解两种橙子市场销售情况，购进了一批数量相等的“血橙”和“脐橙”供客户对比品尝，其中购买“脐橙”用了420元，购买“血橙”用了756元，已知每千克“血橙”进价比每千克“脐橙”贵8元．
(1)求每千克“血橙”和“脐橙”进价各是多少元？
(2)若该水果商城决定再次购买同种“血橙”和“脐橙”共40千克，且再次购买的费用不超过600元，且每种橙子进价保持不变．若“血橙”的销售单价为24元，“脐橙”的销售单价为14元，则该水果商城应如何进货，使得第二批的“血橙”和“脐橙”售完后获得利润最大？最大利润是多少？

21．如图，在△ABC中，点D、E分别为BC、AC的中点，过点A作BC的平行线，交DE的延长线于点F，连接AD、CF．
(1)求证：△AEF≌△CED；
(2)若∠BAC=90°，则四边形ADCF是，什么特殊四边形？请说明理由．

22．2022年冬奥会成功在北京张家口举行，奥林匹克精神鼓舞了越来越多的年轻人从事冰雪运动．在长8m，高6m的斜面上，滑雪运动员P从顶端腾空而起，最终刚好落在斜面底端，其轨迹可视为抛物线的一部分．按如图方式建立平面直角坐标系，设斜面所在直线的函数关系式为y₁=kx+b，运动员轨迹所在抛物线的函数关系式为y₂=ax²+x+c，设运动员P距离地面的高度为h(m)，腾空过程中离开斜面的距离为d(m)，回答下列问题：
(1)分别求出y₁、y₂与x之间的函数关系式；
(2)求出h的最大值和此时点P的坐标；
(3)求出d的最大值和此时点P的坐标．

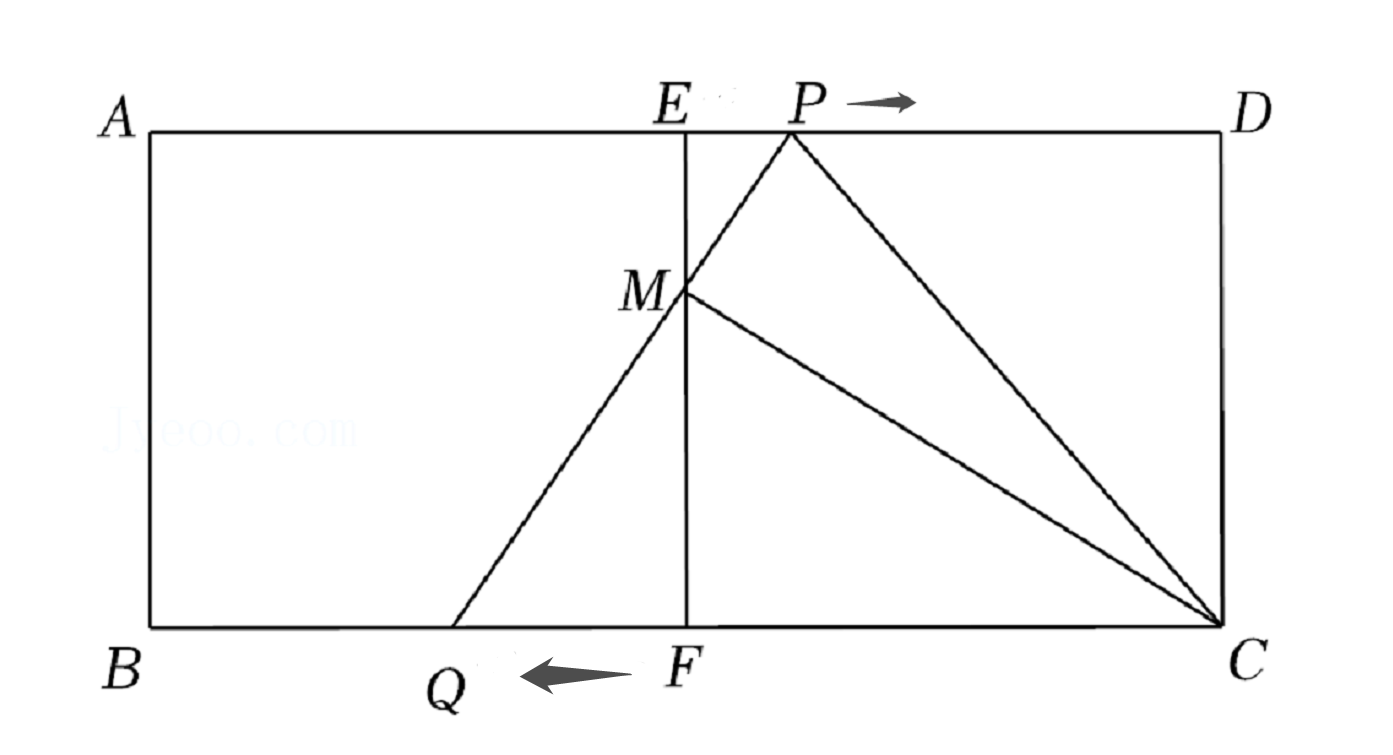
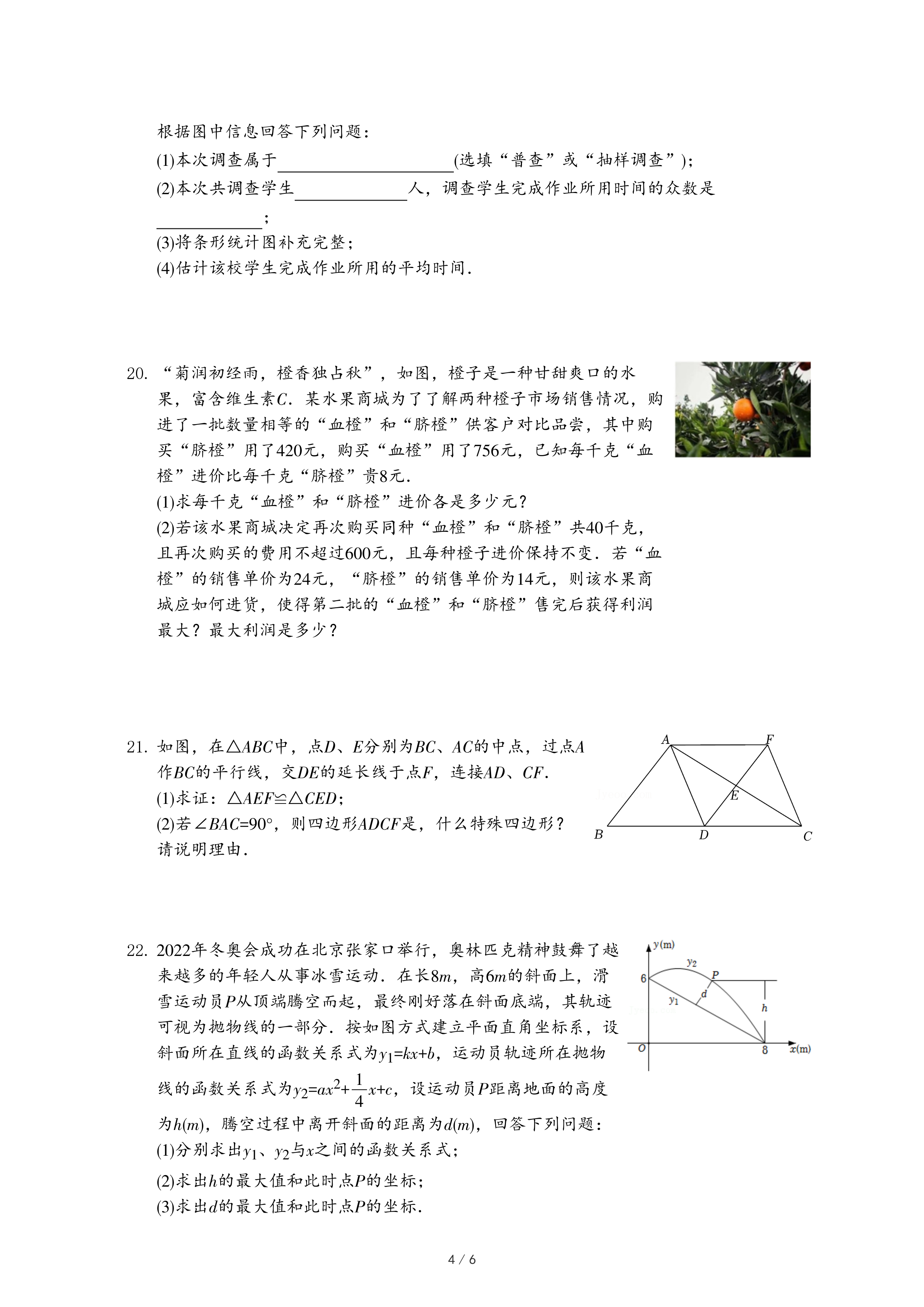
23．问题提出：如图1，在m×n×h个小正方体组成的长方体中，最多能看到多少个小正方体？
研究思路：直接研究这个问题较为复杂，我们可以将问题转化为用小正方体总数减去看不到的小正方体个数，以求得最多能看到的小正方体的个数．
探究一：如图2，在2×2×2的正方体中，有1×1×1=1个小正方体看不到，所以最多能看到2×2×2-1=7个小正方体．
探究二：在3×3×3的正方体中，有2×2×2=8个小正方体看不到，所以最多能看到3×3×3-8=19个小正方体．
(1)探究三：在4×4×4的正方体中，有3×3×3=27个小正方体看不到，所以最多能看      个小正方体．
(2)探究四：在n×n×n的正方体中，有      个小正方体看不到，所以最多能看到      个小正方体．(均化为最简形式)
(3)问题解决：如图3，小明是魔方爱好者，他有一个七阶魔方(7×7×7的正方体)，则他最多能看到      个小正方体．
(4)问题应用：若在n×n×n的正方体中最多能看到217个小正方体，求n的值．(写出解答过程)
(5)探究五：在2×3×4的长方体中，有1×2×3=6个小正方体看不到，所以最多能看到      个小正方体．
(6)探究六：在m×n×h的长方体中，最多能看到      个小正方体．(化为最简形式)
(7)拓展延伸：小明在研究m×n×h的长方体时，他最多能看到a个小正方体，此时他看不到12个小正方体，则a有      种可能取值，a的最小值是      ．
(1)

24．如图，在矩形ABCD中，AB=9，AD=26．点E、F分别为AD、BC的中点．动点P从点E出发，以1个单位长度每秒的速度向点D运动；动点Q从点F出发，以2个单位长度每秒的速度向点B运动．连接EF、PQ相交于点M，连接CP、CM．设运动时间为t(s)(0＜t＜)，回答下列问题：
(1)t为何值时，点P在线段CQ的垂直平分线上？
(2)设△PMC的面积为S，求出S与t之间的函数关系式；
(3)t为何值时，CM⊥PQ？
(4)作点C关于直线PQ的对称点C′，是否存在某一时刻t，使得点C′落在直线AD上？若存在，求出t的值；若不存在，请说明理由．