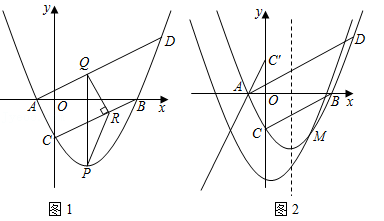
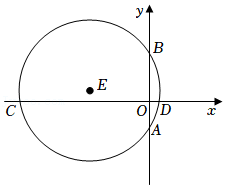
24.如图,已知抛物线y=ax
2+bx-4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-2,0),直线BC的解析式为y=
x-4.
(1)求抛物线的解析式.
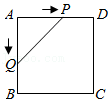
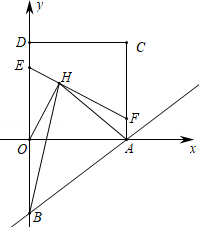
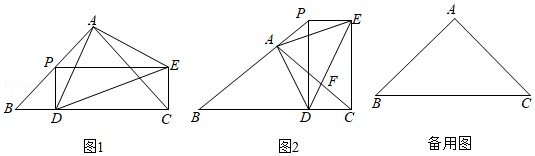
(2)如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标.
(3)如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2
√5
个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.