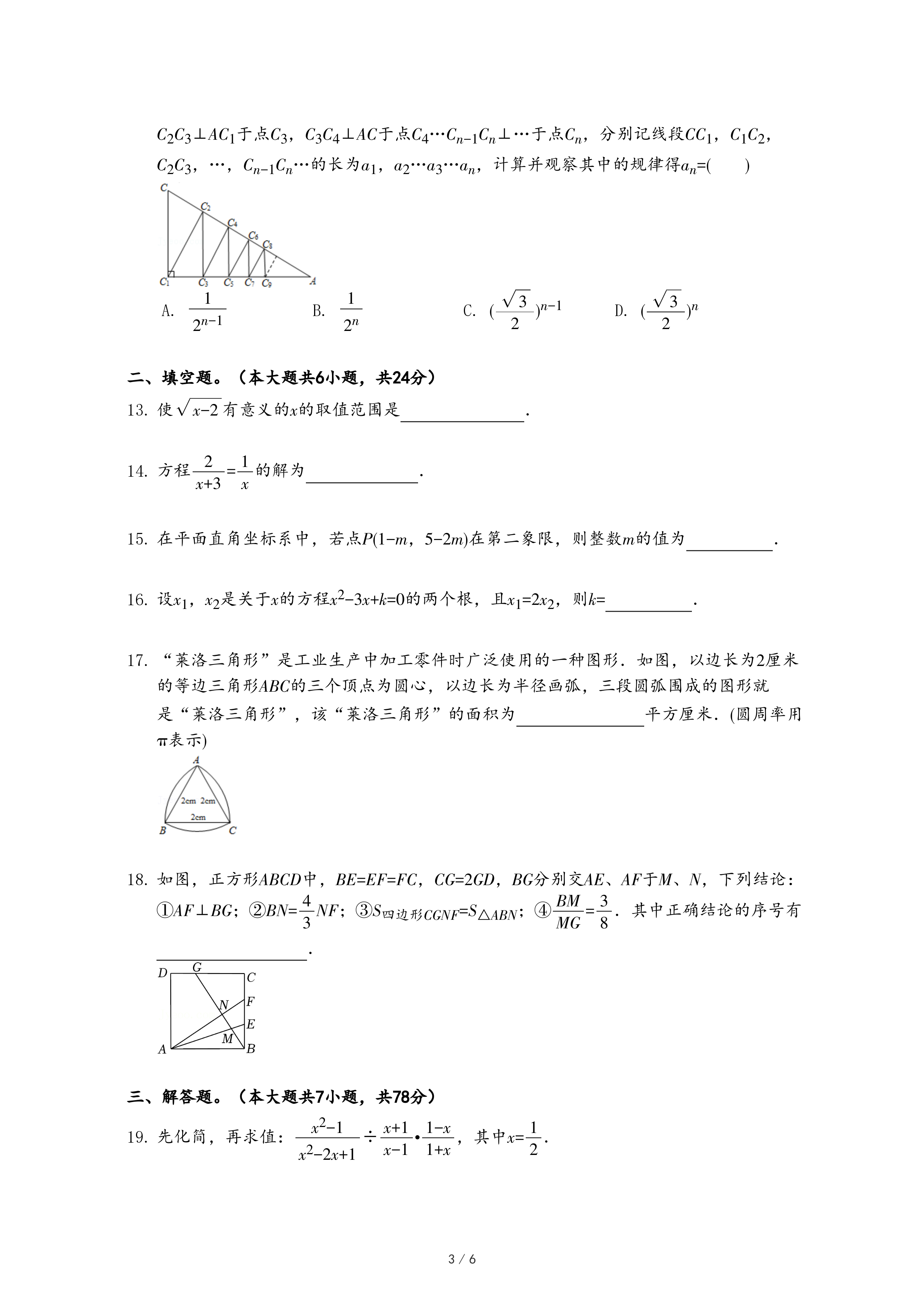




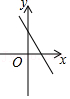
| k |
| x |
| 1 |
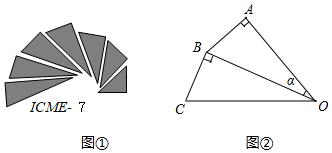
| sinα |
| 1080 |
| x |
| 1080 |
| x-15 |
| 1080 |
| x |
| 1080 |
| x-15 |
| 1080 |
| x+15 |
| 1080 |
| x |
| 1080 |
| x+15 |
| 1080 |
| x |
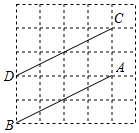
| 4 √5 |
| 5 |
| 3 √5 |
| 5 |
| x | … | -2 | 0 | 1 | 3 | … |
| y | … | 6 | -4 | -6 | -4 | … |
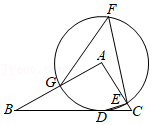
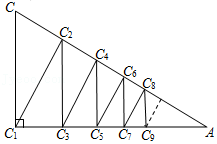
| 1 |
| 2n-1 |
| 1 |
| 2n |
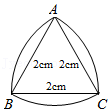
√3 |
| 2 |
√3 |
| 2 |
| 2 |
| x+3 |
| 1 |
| x |
| 4 |
| 3 |
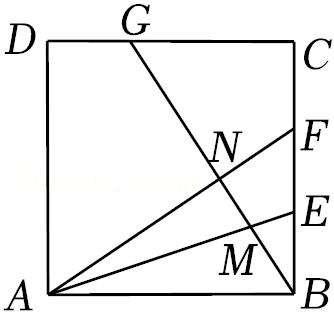
| BM |
| MG |
| 3 |
| 8 |
| x2-1 |
| x2-2x+1 |
| x+1 |
| x-1 |
| 1-x |
| 1+x |
| 1 |
| 2 |
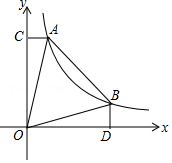
| k |
| x |
| 包装袋型号 | A | B |
| 甲类农产品质量(千克) | 2x | |
| 乙类农产品质量(千克) | 5(90-y) |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |