24.小超在观看足球比赛时,发现了这样一个问题:两名运动员从不同的位置出发,沿着不同的方向,以不同的速度直线奔跑,什么时候他们离对方最近呢?
小超通过一定的测量,并选择了合适的比例尺,把上述问题抽象成如下数学问题:
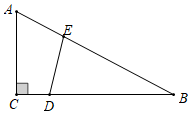
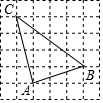
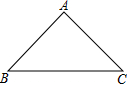
如图,在
Rt△ABC中,∠C=90°,AC=6
cm,BC=8
cm,点D以1
cm/s的速度从点C向点B运动,点E以2
cm/s的速度从点A向点B运动,当点E到达点B时,两点同时停止运动,若点D,E同时出发,多长时间后DE取得最小值?
小超猜想当DE⊥AB时,DE最小,探究后发现用几何的知识解决这个问题有一定的困难,于是根据函数的学习经验,设C,D两点间的距离为x
cm,D,E两点间的距离为y
cm,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)由题意可知线段AE和CD的数量关系是
;
(2)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
| y/cm | 6.0 | 4.8 | 3.8 | | 2.7 | 3.0 |
(说明:补全表格时相关数值保留一位小数)
(3)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题,小组的猜想
;(填“正确”或“不正确”)当两点同时出发了
s时,DE取得最小值,为
cm.