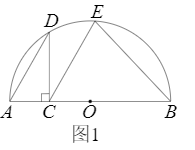
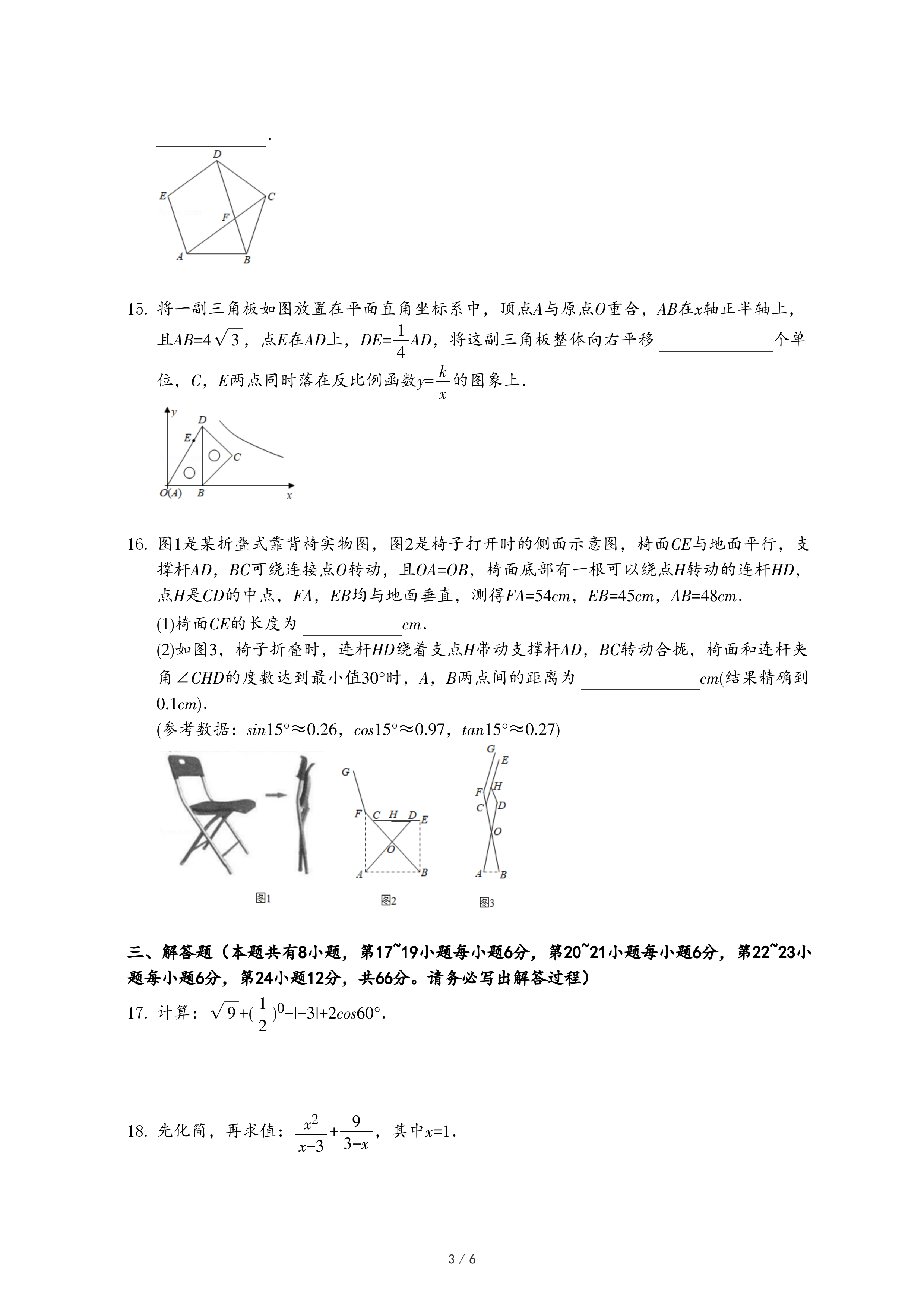
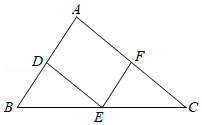
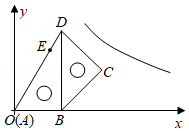
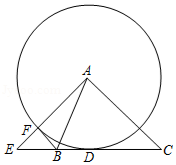
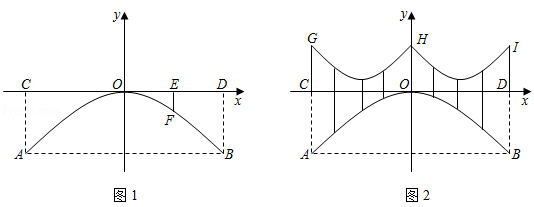
23.如图1,点C是半圆O的直径AB上一动点(不包括端点),AB=6
cm,过点C作CD⊥AB交半圆于点D,连结AD,过点C作CE∥AD交半圆于点E,连结EB.牛牛想探究在点C运动过程中EC与EB的大小关系.他根据学习函数的经验,记AC=x
cm,EC=y
1cm,EB=y
2cm.请你一起参与探究函数y
1、y
2随自变量x变化的规律.
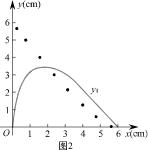
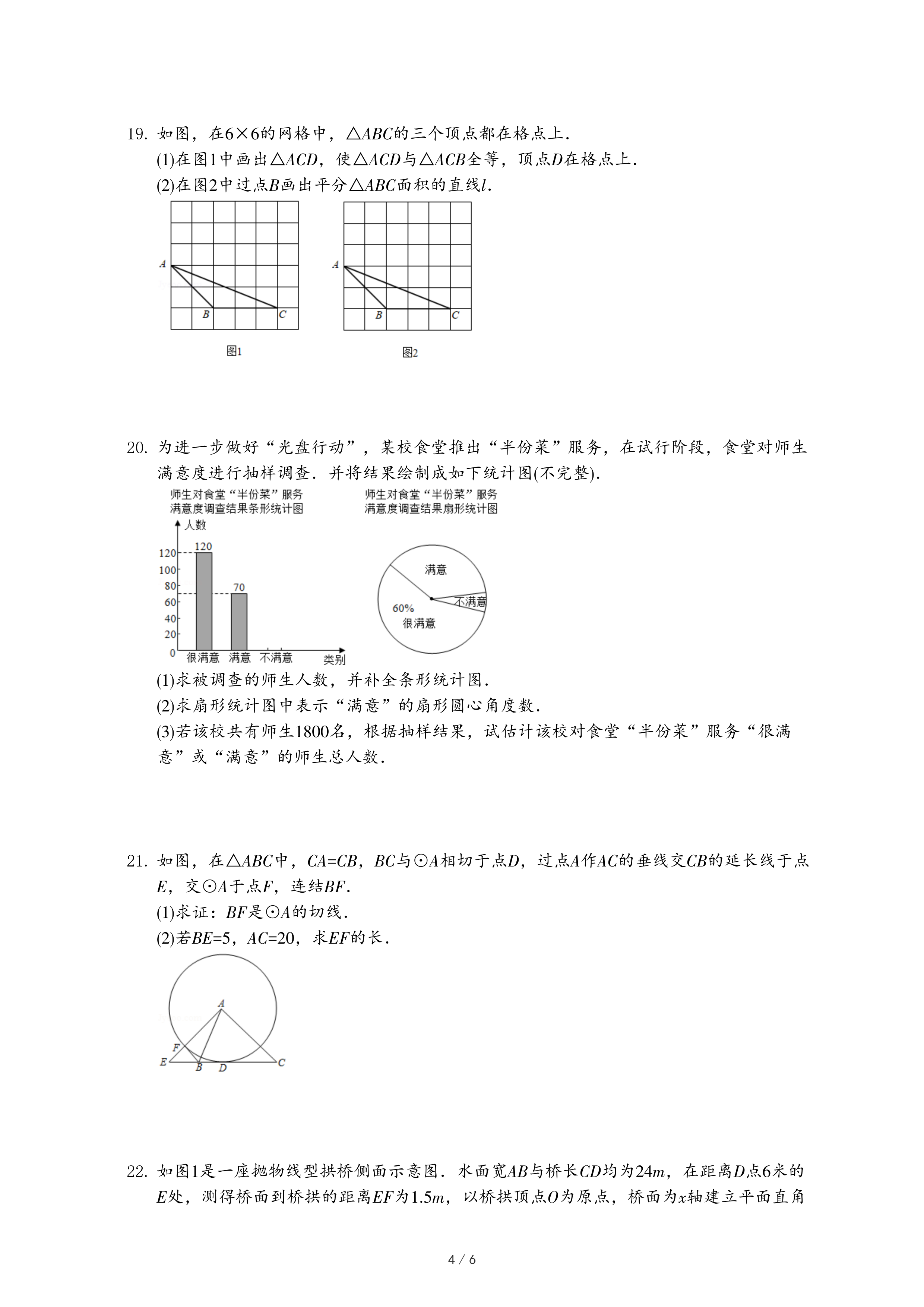
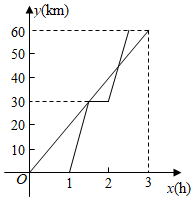
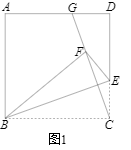
通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
| x | … | 0.30 | 0.80 | 1.60 | 2.40 | 3.20 | 4.00 | 4.80 | 5.60 | … |
| y1 | … | 2.01 | 2.98 | 3.46 | 3.33 | 2.83 | 2.11 | 1.27 | 0.38 | … |
| y2 | … | 5.60 | 4.95 | 3.95 | 2.96 | 2.06 | 1.24 | 0.57 | 0.10 | … |
(1)当x=3时,y
1=
.
(2)在图2中画出函数y
2的图象,并结合图象判断函数值y
1与y
2的大小关系.
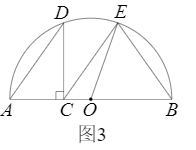
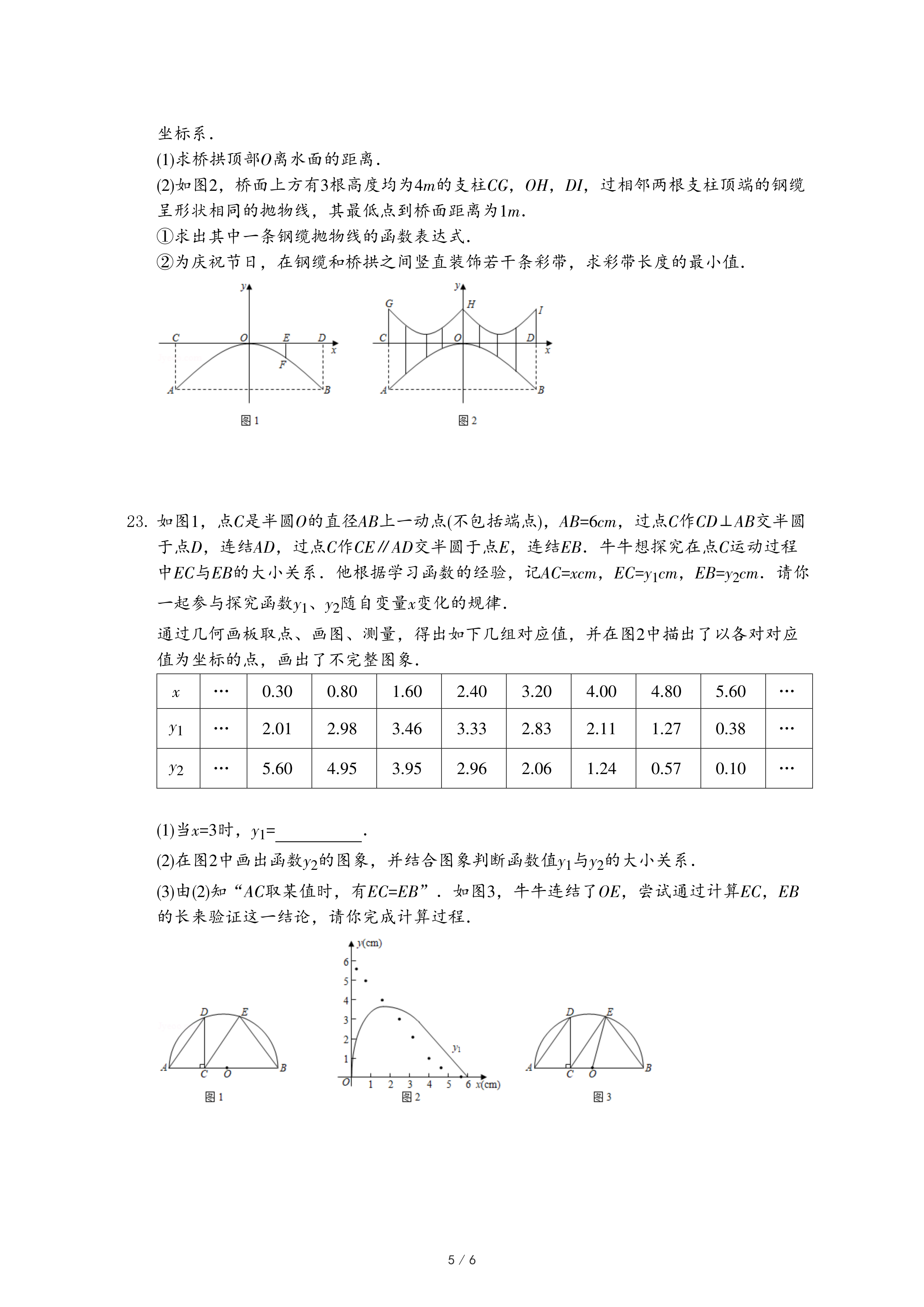
(3)由(2)知“AC取某值时,有EC=EB”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.