17．(1)计算：4sin60°-+(2-)⁰．
(2)解不等式：5x+3≥2(x+3)．

18．绍兴莲花落，又称“莲花乐”，“莲花闹”，是绍兴一带的曲艺．为了解学生对该曲种的熟悉度，某校设置了：非常了解、了解、了解很少、不了解四个选项，随机抽查了部分学生进行问卷调查，要求每名学生只选其中的一项，并将抽查结果绘制成不完整的统计图．

根据图中信息，解答下列问题：
(1)本次接受问卷调查的学生有多少人？并求图2中“了解”的扇形圆心角的度数；
(2)全校共有1200名学生，请你估计全校学生中“非常了解”、“了解”莲花落的学生共有多少人．

19．Ⅰ号无人机从海拔10m处出发，以10m/min的速度匀速上升，Ⅱ号无人机从海拔30m处同时出发，以a(m/min)的速度匀速上升，经过5min两架无人机位于同一海拔高度b(m)．无人机海拔高度y(m)与时间x(min)的关系如图．两架无人机都上升了15min．
(1)求b的值及Ⅱ号无人机海拔高度y(m)与时间x(min)的关系式；
(2)问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高28米．

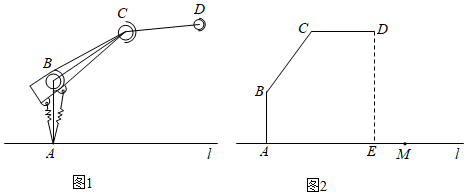
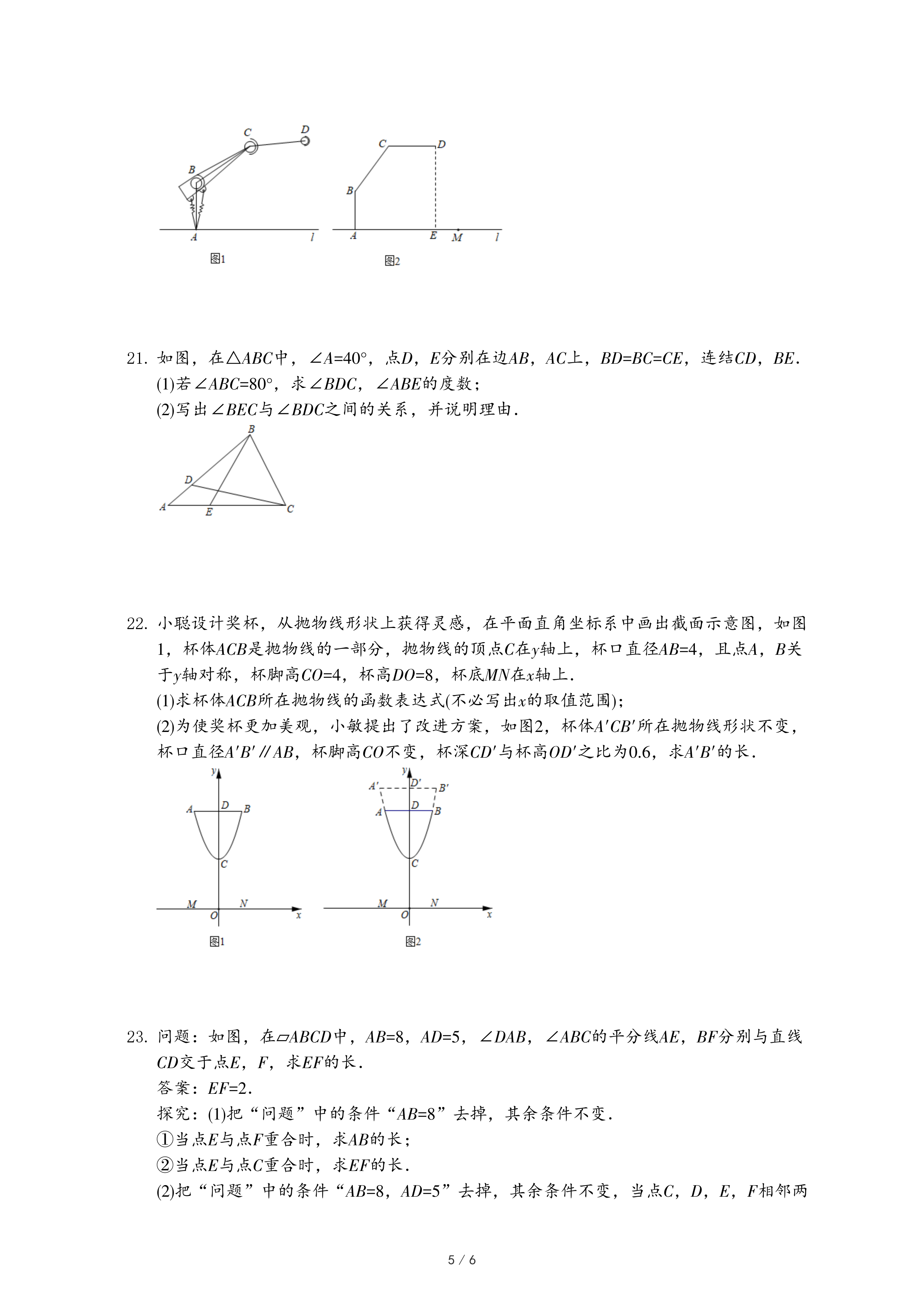
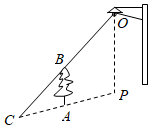
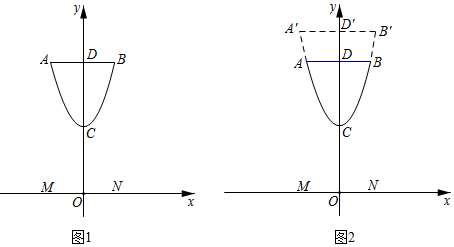
20．拓展小组研制的智能操作机器人，如图1，水平操作台为l，底座AB固定，高AB为50cm，连杆BC长度为70cm，手臂CD长度为60cm．点B，C是转动点，且AB，BC与CD始终在同一平面内．
(1)转动连杆BC，手臂CD，使∠ABC=143°，CD∥l，如图2，求手臂端点D离操作台l的高度DE的长(精确到1cm，参考数据：sin53°≈0.8，cos53°≈0.6)．
(2)物品在操作台l上，距离底座A端110cm的点M处，转动连杆BC，手臂CD，手臂端点D能否碰到点M？请说明理由．

21．如图，在△ABC中，∠A=40°，点D，E分别在边AB，AC上，BD=BC=CE，连结CD，BE．
(1)若∠ABC=80°，求∠BDC，∠ABE的度数；
(2)写出∠BEC与∠BDC之间的关系，并说明理由．

22．小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体ACB是抛物线的一部分，抛物线的顶点C在y轴上，杯口直径AB=4，且点A，B关于y轴对称，杯脚高CO=4，杯高DO=8，杯底MN在x轴上．
(1)求杯体ACB所在抛物线的函数表达式(不必写出x的取值范围)；
(2)为使奖杯更加美观，小敏提出了改进方案，如图2，杯体A′CB′所在抛物线形状不变，杯口直径A′B′∥AB，杯脚高CO不变，杯深CD′与杯高OD′之比为0.6，求A′B′的长．

23．问题：如图，在▱ABCD中，AB=8，AD=5，∠DAB，∠ABC的平分线AE，BF分别与直线CD交于点E，F，求EF的长．
答案：EF=2．
探究：(1)把“问题”中的条件“AB=8”去掉，其余条件不变．
①当点E与点F重合时，求AB的长；
②当点E与点C重合时，求EF的长．
(2)把“问题”中的条件“AB=8，AD=5”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求的值．

24．如图，矩形ABCD中，AB=4，点E是边AD的中点，点F是对角线BD上一动点，∠ADB=30°．连结EF，作点D关于直线EF的对称点P．
(1)若EF⊥BD，求DF的长；
(2)若PE⊥BD，求DF的长；
(3)直线PE交BD于点Q，若△DEQ是锐角三角形，求DF长的取值范围．