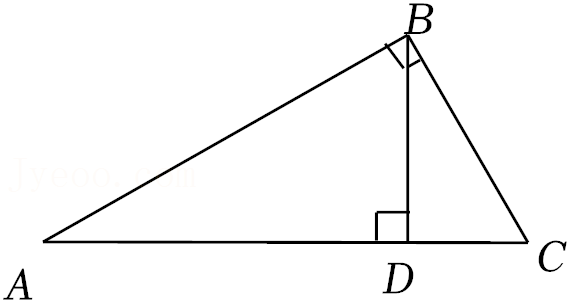
17．《几何原本》是一部集前人思想和欧几里得个人创造性一体的不朽之作，把人们公认的一些事实列成定义、公理和公设，用它们来研究各种几何图形的性质，从而建立了一套从定义、公理和公设出发，论证命题得到定理的几何学论证方法．小牧在学习过程中产生了一个猜想：“如果三角形一边上的中线的长度等于所在边长度的一半，那么这个三角形是直角三角形．”
(1)请你用尺规作图，在图中作出线段AB的中点D，并连接CD．(保留作图痕迹)

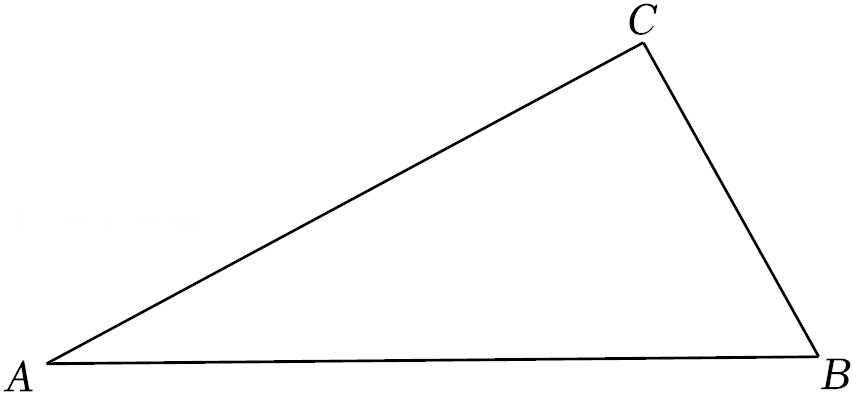
(2)请你结合图形，将小牧猜想的命题写成已知、求证．
已知：      ．
求证：△ABC为直角三角形．
(3)补全上述猜想的证明过程．
证明：∵点D是线段AB的中点，
∴AD=BD，
又∵CD=AB，
∴AD=BD=CD．
在△ACD中，AD=CD，
∴∠DCA=∠A，(      )，
同理，在△BCD中，∠DCB=∠B．
在△ABC中，
∵∠DCA+∠A+∠DCB+∠B=180°．
∴      ，
∴在△ABC中，∠ACB=90°，
∴△ABC为直角三角形．

18．计算：-×(+3)．

19．计算：-(π-5)⁰+()^-2．

20．已知m+2n=，求代数式(+2)÷的值．

21．解方程：-1=．

22．已知：如图，△ABC中，AB=AC，BE，CD分别是∠ABC，∠ACB的平分线．请你写出图中的一对全等三角形，并证明．

23．如图是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点为格点，线段AB的端点都在格点上．要求以AB为边画一个等腰△ABC，且使得点C为格点．请在下面的网格图中画出3种不同的等腰△ABC．

24．某种型号的LED显示屏为长方形，其长与宽的比为4:3；若将该显示屏的长、宽各减少2cm，则其长与宽的比值将会变为3:2．求该型号LED显示屏的长度与宽度．

25．如图，在△ABC中，∠C=90°，AC=BC，在△ABD中，∠D=90°，AD与BC交于点E，且∠DBE=∠DAB．
求证：
(1)∠CAE=∠DBC；
(2)AC²+CE²=4BD²．

26．北宋科学家沈括在《梦溪笔谈》中曾记载了宋代行军时的后勤供应情况：人负米六斗，卒自携一斗，人食日二升．其大意为，在行军过程中，民夫可以背负六斗(60升)米，士兵可以自己背一斗(10升)米，民夫(士兵)每人一天行军会消耗2升米．
(1)若每个士兵雇佣4个民夫随其一同行军，则在没有其他粮食补充的情况下，背负的米支持行军的天数为      天；
(2)若每个士兵雇佣n个民夫随其一同行军，则在没有其他粮食补充的情况下，背负的米支持行军的天数为 ________(用含有n的代数式表示)；如果每个士兵雇佣的民夫数量没有上限，在没有其他粮食补充的情况下，背负的米支持的行军天数有没有上限？________(回答“有”或者“没有” )请你说明理由．

27．如图，∠HAB=30°，点B与点C关于射线AH对称，连接AC．D点为射线AH上任意一点，连接CD．将线段CD绕点C顺时针旋转60°，得到线段CE，连接BE．
(1)求证：直线EB是线段AC的垂直平分线；
(2)点D是射线AH上一动点，请你直接写出∠ADC与∠ECA之间的数量关系．