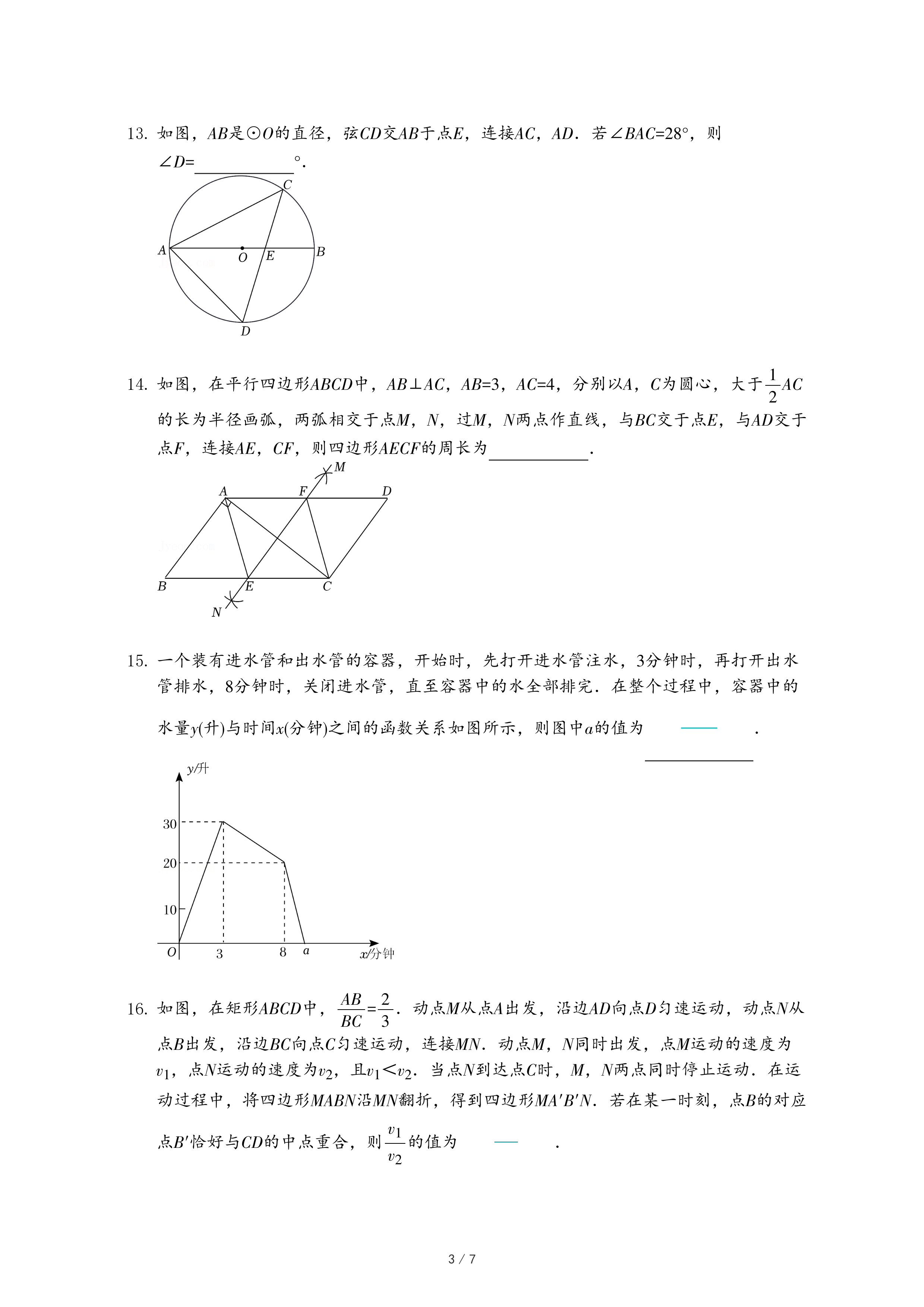



| 2 |
| 3 |



| π |
| 12 |
| π |
| 24 |
√10 π |
| 60 |
√5 π |
| 60 |
| 60 |
| 100 |
| 60 |
| 100 |
| 100 |
| 60 |
| 100 |
| 60 |
| 4 √3 |
| 3 |
| 2 √21 |
| 3 |
| 5 √3 |
| 3 |
| 4 √21 |
| 3 |
| x2 |
| x-2 |
| 2x |
| x-2 |

| 1 |
| 2 |


| AB |
| BC |
| 2 |
| 3 |
| v1 |
| v2 |

| x |
| x+1 |
| 3 |
| x |
| 2 |
| 3 |

| 培训前 | 成绩(分) | 6 | 7 | 8 | 9 | 10 |
| 划记 |    |  |   |  |  | |
| 人数(人) | 12 | 4 | 7 | 5 | 4 | |
| 培训后 | 成绩(分) | 6 | 7 | 8 | 9 | 10 |
| 划记 |  | 一 |  |   |    | |
| 人数(人) | 4 | 1 | 3 | 9 | 15 |
| m |
| x |
| 7 |
| 2 |


| 进货批次 | 甲种水果质量(单位:千克) | 乙种水果质量(单位:千克) | 总费用(单位:元) |
| 第一次 | 60 | 40 | 1520 |
| 第二次 | 30 | 50 | 1360 |

| 3 |
| 2 |
| AB |
| AD |
| BE |
| DE |
| 9 |
| 16 |

