






| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |

| 近视眼镜的度数y(度) | 200 | 250 | 400 | 500 | 1000 |
| 镜片焦距x(米) | 0.50 | 0.40 | 0.25 | 0.20 | 0.10 |
| 100 |
| x |
| x |
| 100 |
| 400 |
| x |
| x |
| 400 |
| 3 |
| 2 |
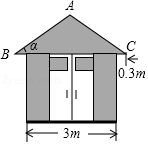
| 9 |
| 5sinα |
| 9 |
| 5cosα |
| 9 |
| 9sinα |
| 5 |
| 5cosα |
| S1 |
| S2 |
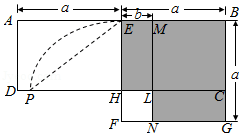
√2 |
| 2 |
√2 |
| 3 |
√2 |
| 4 |
√2 |
| 6 |
| { | x+2>3
|

| x+4 |
| x2+3x |
| 1 |
| x2+3x |

| 生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
| 工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
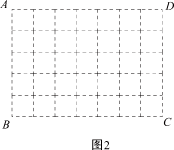
| 1 |
| 2 |

| 3 |
| 8 |
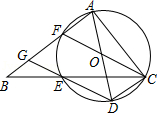
| 1 |
| 2 |
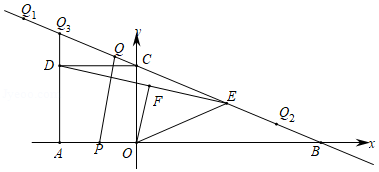
| n |
| m |
| 1 |
| 7 |