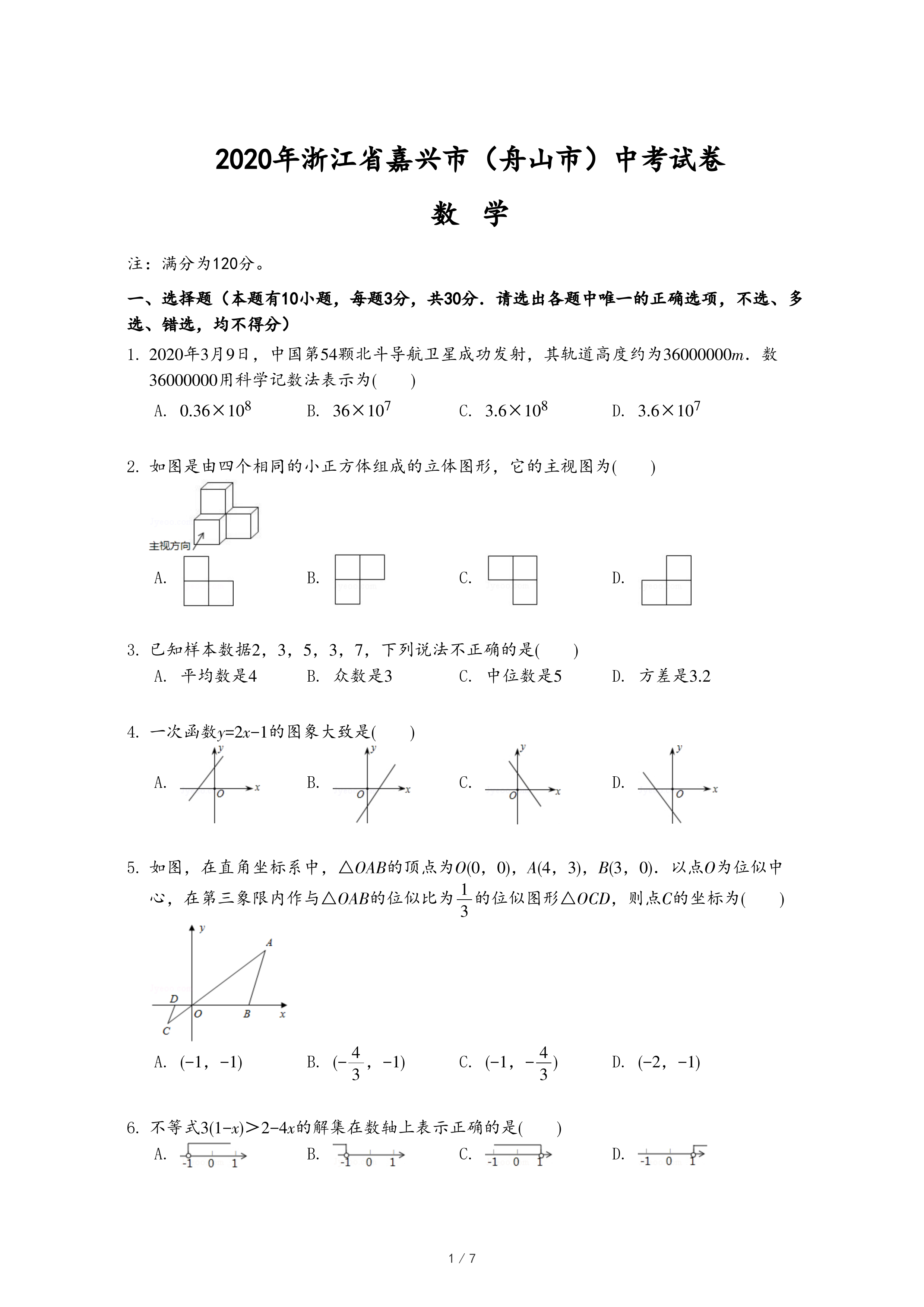





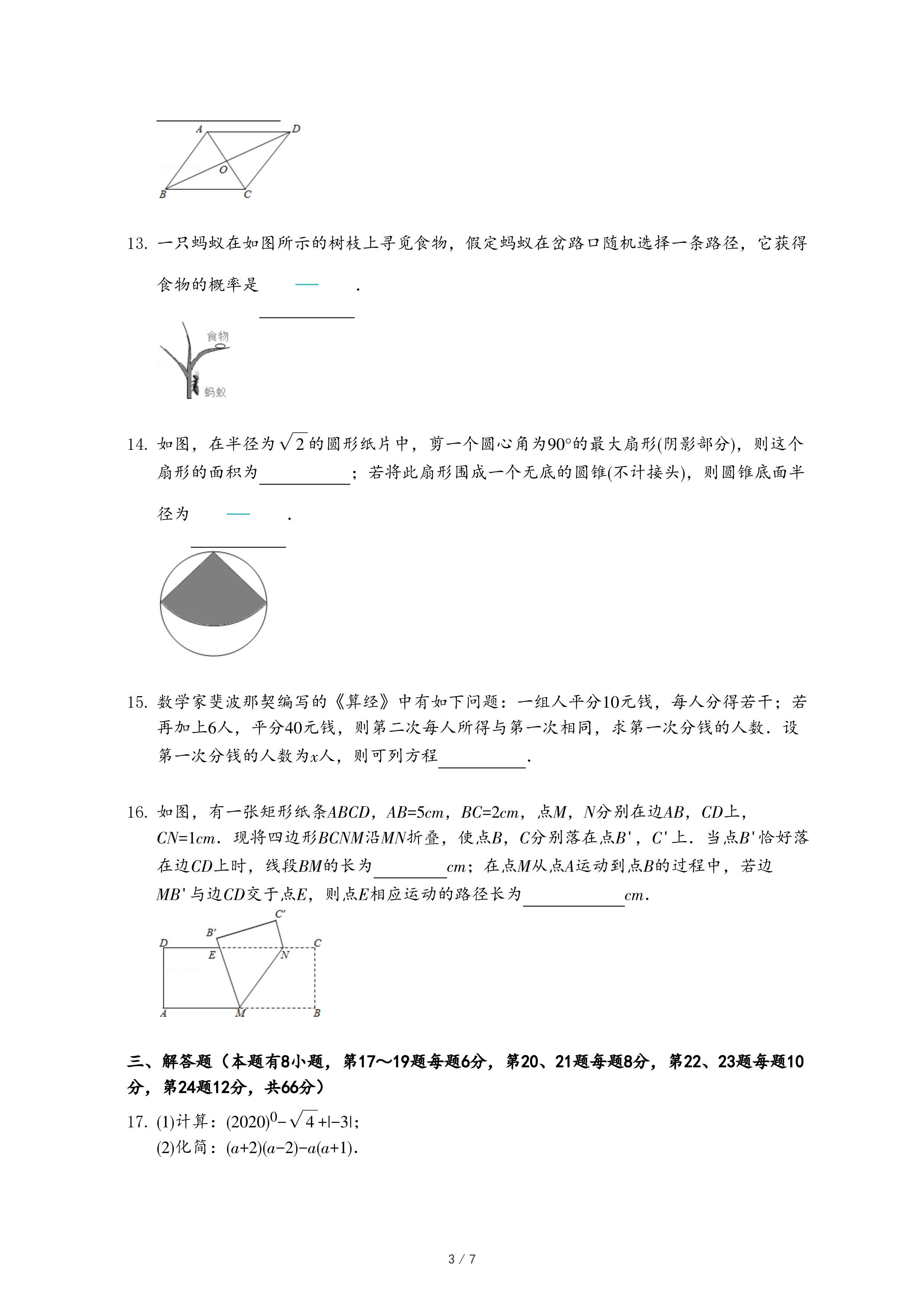



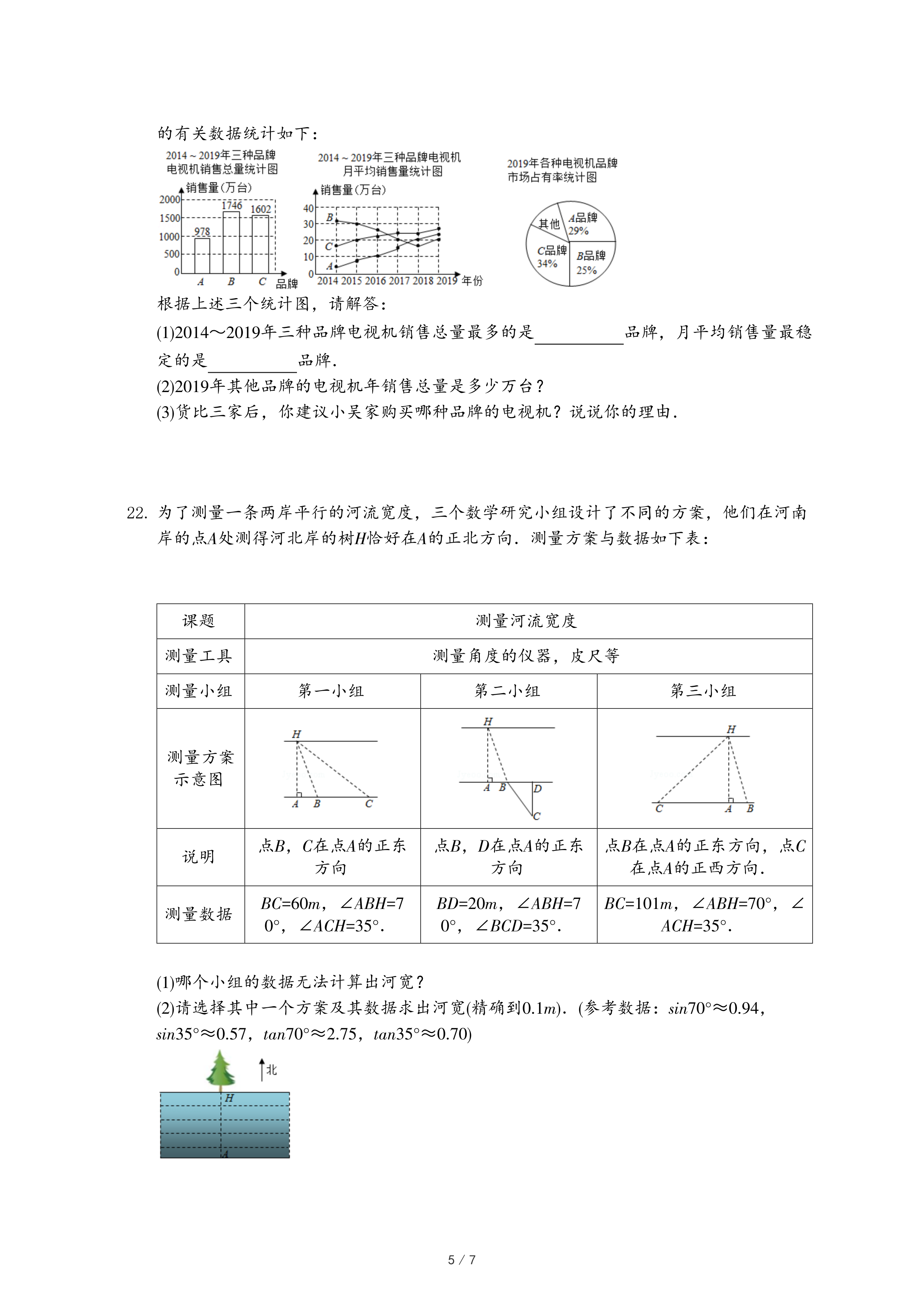

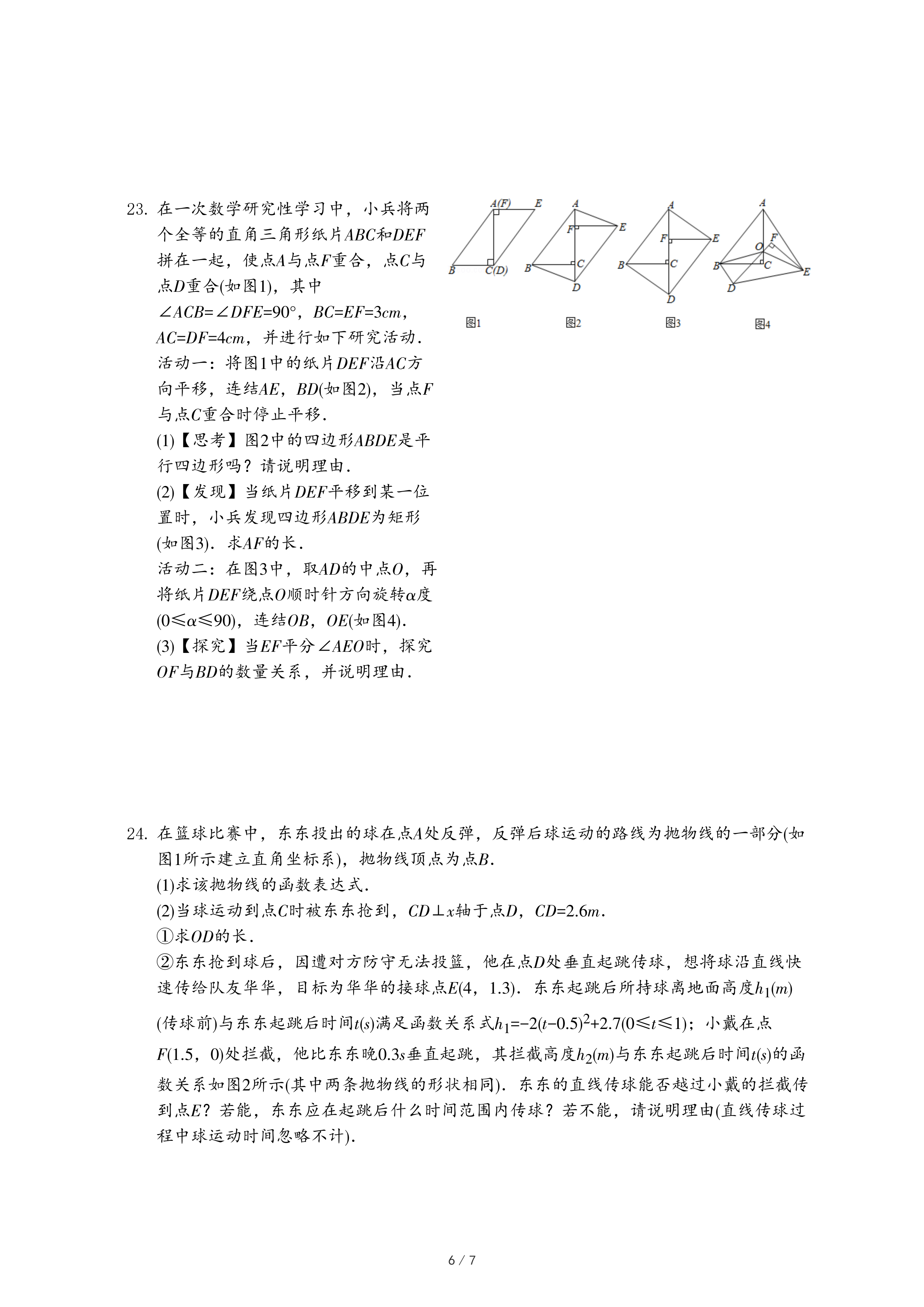











| 1 |
| 3 |

| 4 |
| 3 |
| 4 |
| 3 |





| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |





| 证明:连结OC,∵OA=OB,∴∠A=∠B,又∵OC=OC,∴△OAC≌△OBC,∴AC=BC. |

| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 6 | 2.9 | 2 | 1.5 | 1.2 | 1 |


| 课题 | 测量河流宽度 | ||
| 测量工具 | 测量角度的仪器,皮尺等 | ||
| 测量小组 | 第一小组 | 第二小组 | 第三小组 |
| 测量方案示意图 |  |  |  |
| 说明 | 点B,C在点A的正东方向 | 点B,D在点A的正东方向 | 点B在点A的正东方向,点C在点A的正西方向. |
| 测量数据 | BC=60m,∠ABH=70°,∠ACH=35°. | BD=20m,∠ABH=70°,∠BCD=35°. | BC=101m,∠ABH=70°,∠ACH=35°. |


