2019-2020学年北京市西城区九年级（上）期末数学试卷-乐乐课堂

1．如图，四边形ABCD内接于⊙O，若∠ADC=80°，则∠ABC的度数是(　　)

A. 40°
B. 80°
C. 100°
D. 120°

2．在平面直角坐标系中，将抛物线y=x²向右平移2个单位长度，向上平移1个单位长度，得到抛物线(　　)

A. y=(x-2)²+1
B. y=(x-2)²-1
C. y=(x+2)²+1
D. y=(x+2)²-1

3．圆心角是90°，半径为20的扇形的弧长为(　　)

A. 5π
B. 10π
C. 20π
D. 25π

4．如图，在△ABC中，以C为中心，将△ABC顺时针旋转35°得到△DEC，边ED，AC相交于点F，若∠A=30°，则∠EFC的度数为(　　)

A. 60°
B. 65°
C. 72.5°
D. 115°

5．如图，AB是⊙O的直径，弦CD⊥AB于E，若∠ABC=30°，OE=

√3

，则OD长为(　　)

A. 3
B.
√6
C. 2
√3
D. 2

6．下列关于抛物线y=x²+bx-2的说法正确的是(　　)

A. 抛物线的开口方向向下
B. 抛物线与y轴交点的坐标为(0，2)
C. 当b＞0时，抛物线的对称轴在y轴右侧
D. 对于任意的实数b，抛物线与x轴总有两个公共点

7．A(-

1

2

，y₁)，B(1，y₂)，C(4，y₃)三点都在二次函数y=-(x-2)²+k的图象上，则y₁，y₂，y₃的大小关系为(　　)

A. y₁＜y₂＜y₃
B. y₁＜y₃＜y₂
C. y₃＜y₁＜y₂
D. y₃＜y₂＜y₁

8．如图，AB=5，O是AB的中点，P是以点O为圆心，AB为直径的半圆上的一个动点(点P与点A，B可以重合)，连接PA，过P作PM⊥AB于点M．设AP=x，AP-AM=y，则下列图象中，能表示y与x的函数关系的图象大致是(　　)

A.
B.
C.
D.

9．函数y=ax²+bx+c(0≤x≤3)的图象如图所示，则该函数的最小值是．

10．如图，在△ABC中，点D，E分别在边AB，AC上，添加一个条件使得△ADE∽△ACB，添加的一个条件是．

11．如图，△ABO三个顶点的坐标分别为A(-2，4)，B(-4，0)，O(0，0)，以原点O为位似中心，画出一个三角形，使它与△ABO的相似比为

1

2

．

12．如图，A，B两点的坐标分别为A(3，0)，B(0，

√3

)，将线段BA绕点B顺时针旋转得到线段BC．若点C恰好落在x轴的负半轴上，则旋转角为 °．

13．在“测量学校教学楼的高度”的数学活动中，小刚同学使用镜面反射法进行测量，如图所示．若a₁=1米，a₂=10米，h=1.5米，则这个学校教学楼的高度为米．

14．我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”，所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率，刘徽计算出圆周率π≈3.14．

刘徽从正六边形开始分割圆，每次边数成倍增加，依次可得圆内接正十二边形，圆内接正二十四边形，…，割的越细，圆的内接正多边形就越接近圆．设圆的半径为R，圆内接正六边形的周长P₆=6R，计算π≈

P₆

2R

=3；圆内接正十二边形的周长P₁₂=24Rsin15°，计算π≈

P₁₂

2R

=3.10；请写出圆内接正二十四边形的周长 P₂₄= ，计算π≈ ．(参考数据：sin15°≈0.258，sin7.5°≈0.130)

15．在关于x的二次函数y=ax²+bx+c中，自变量x可以取任意实数，下表是自变量x与函数y的几组对应值：

x	……	1	2	3	4	5	6	7	8	……
y=ax²+bx+c	……	-3.19	-3.10	-2.71	-2.05	-1.10	0.14	1.47	3.48	……

根据以上信息，关于x的一元二次方程ax²+bx+c=0的两个实数根中，其中的一个实数根约等于 (结果保留小数点后一位小数)．

16．如图，矩形ABCD中，AB=4，BC=6，E是边BC的中点，点P在边AD上，设DP=x，若以点D为圆心，DP为半径的⊙D与线段AE只有一个公共点，则所有满足条件的x的取值范围是．

17．计算3tan30°+4cos45°-2sin60°．

18．已知二次函数y=x²-4x+3．
(1)写出该二次函数图象的对称轴及顶点坐标，再描点画图；
(2)利用图象回答：当x取什么值时，y＜0．

19．如图，在△ABC中，AD平分∠BAC，E是AD上一点，且BE=BD．
(1)求证：△ABE∽△ACD；
(2)若BD=1，CD=2，求

AE

AD

的值．

20．如图，在正方形ABCD中，点E在边AB上，将点E绕点D逆时针旋转得到点F，若点F恰好落在边BC的延长线上，连接DE，DF，EF．
(1)判断△DEF的形状，并说明理由；
(2)若EF=4

√2

，则△DEF的面积为．

21．某校要组织“风华杯”篮球赛，赛制为单循环形式(每两队之间都赛一场)．
(1)如果有4支球队参加比赛，那么共进行场比赛；
(2)如果全校一共进行36场比赛，那么有多少支球队参加比赛？

22．如图，AB是⊙O的直径，PB，PC是⊙O的两条切线，切点分别为B，C．连接PO交⊙O于点D，交BC于点E，连接AC．
(1)求证：OE=

1

2

AC；
(2)若⊙O的半径为5，AC=6，求PB的长．

23．图1是一个倾斜角为α的斜坡的横截面，tanα=

1

2

．斜坡顶端B与地面的距离BC为3米．为了对这个斜坡上的绿地进行喷灌，在斜坡底端安装了一个喷头A，喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分．设喷出水珠的竖直高度为y(单位：米)(水珠的竖直高度是指水珠与地面的距离)，水珠与喷头A的水平距离为x(单位：米)，y与x之间近似满足函数关系y=ax²+bx(a，b是常数，a≠0)，图2记录了x与y的相关数据

(1)求y关于x的函数关系式；
(2)斜坡上有一棵高1.8米的树，它与喷头A的水平距离为2米，通过计算判断从A喷出的水珠能否越过这棵树．

24．如图，四边形ABCD内接于⊙O，∠BAD=90°，AC是对角线．点E在BC的延长线上，且∠CED=∠BAC．
(1)判断DE与⊙O的位置关系，并说明理由；
(2)BA与CD的延长线交于点F，若DE∥AC，AB=4，AD=2，求AF的长．

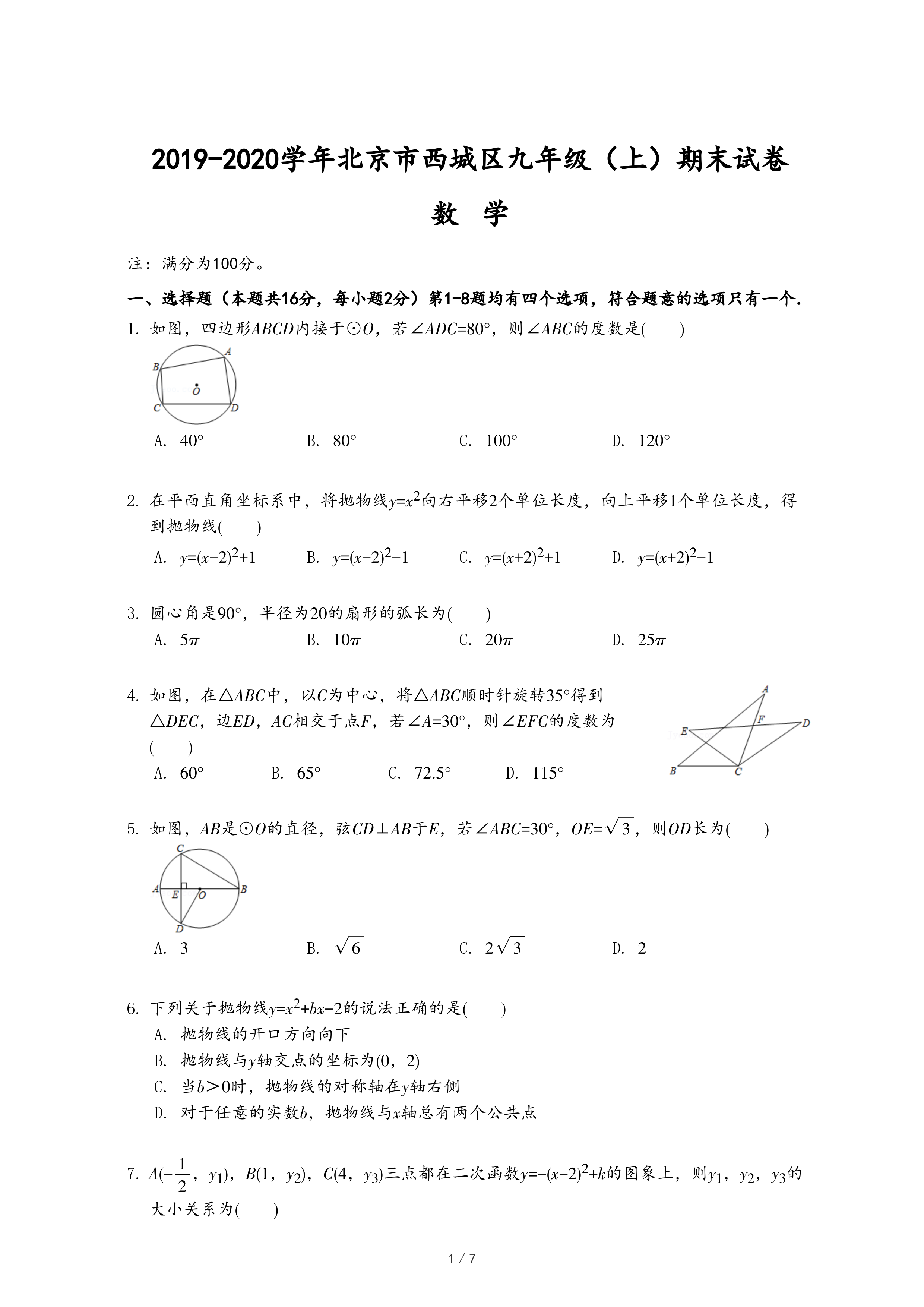
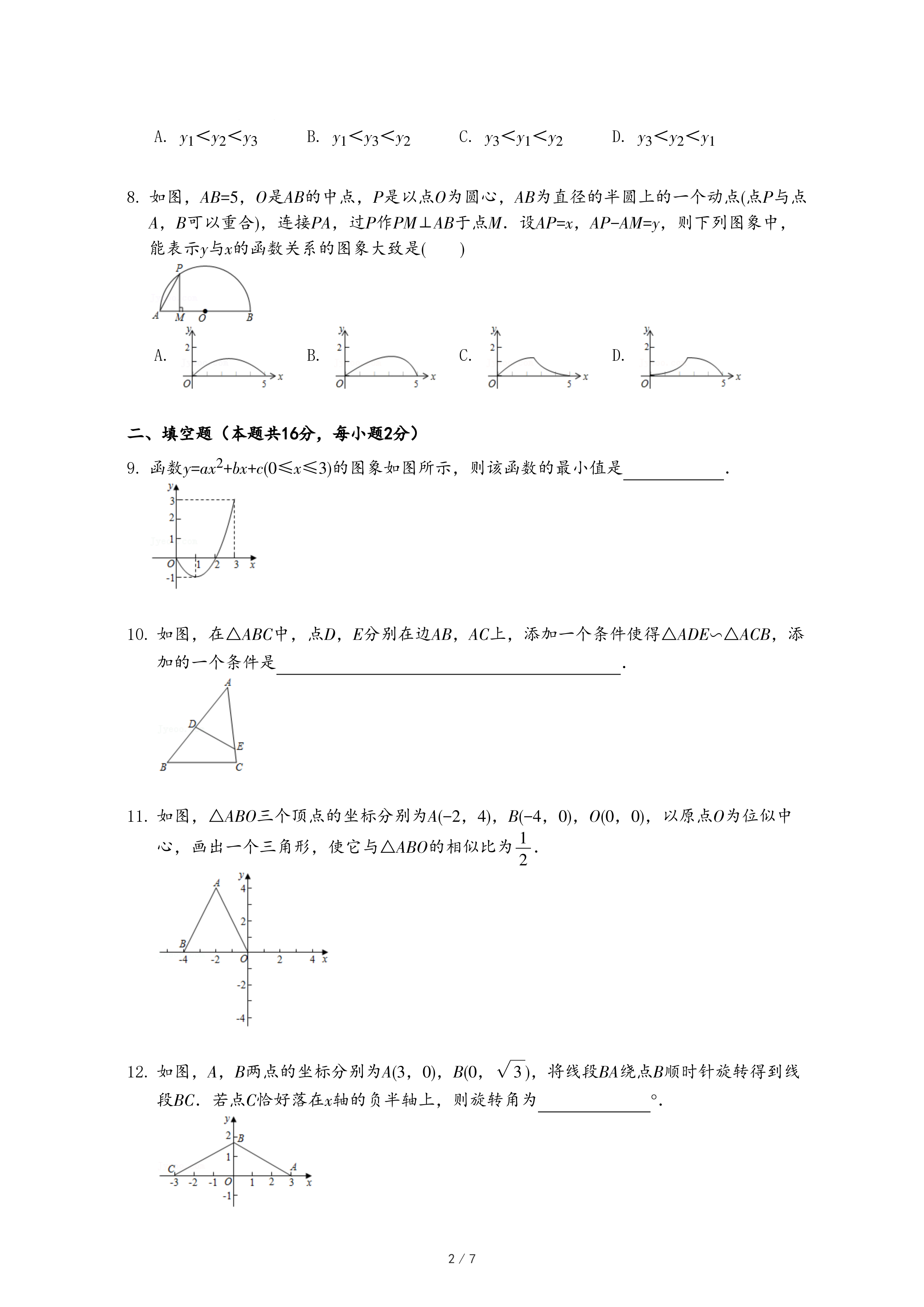
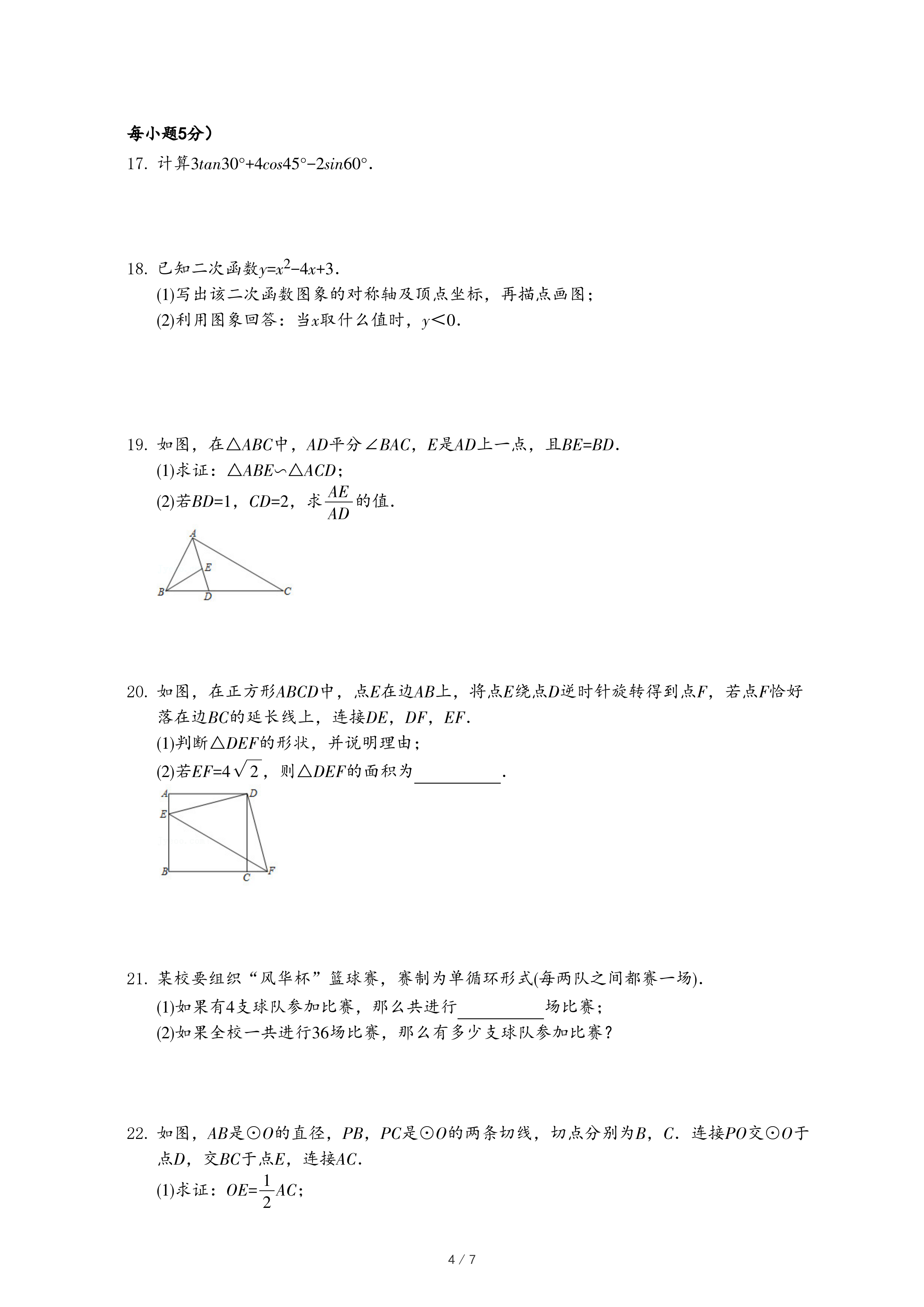
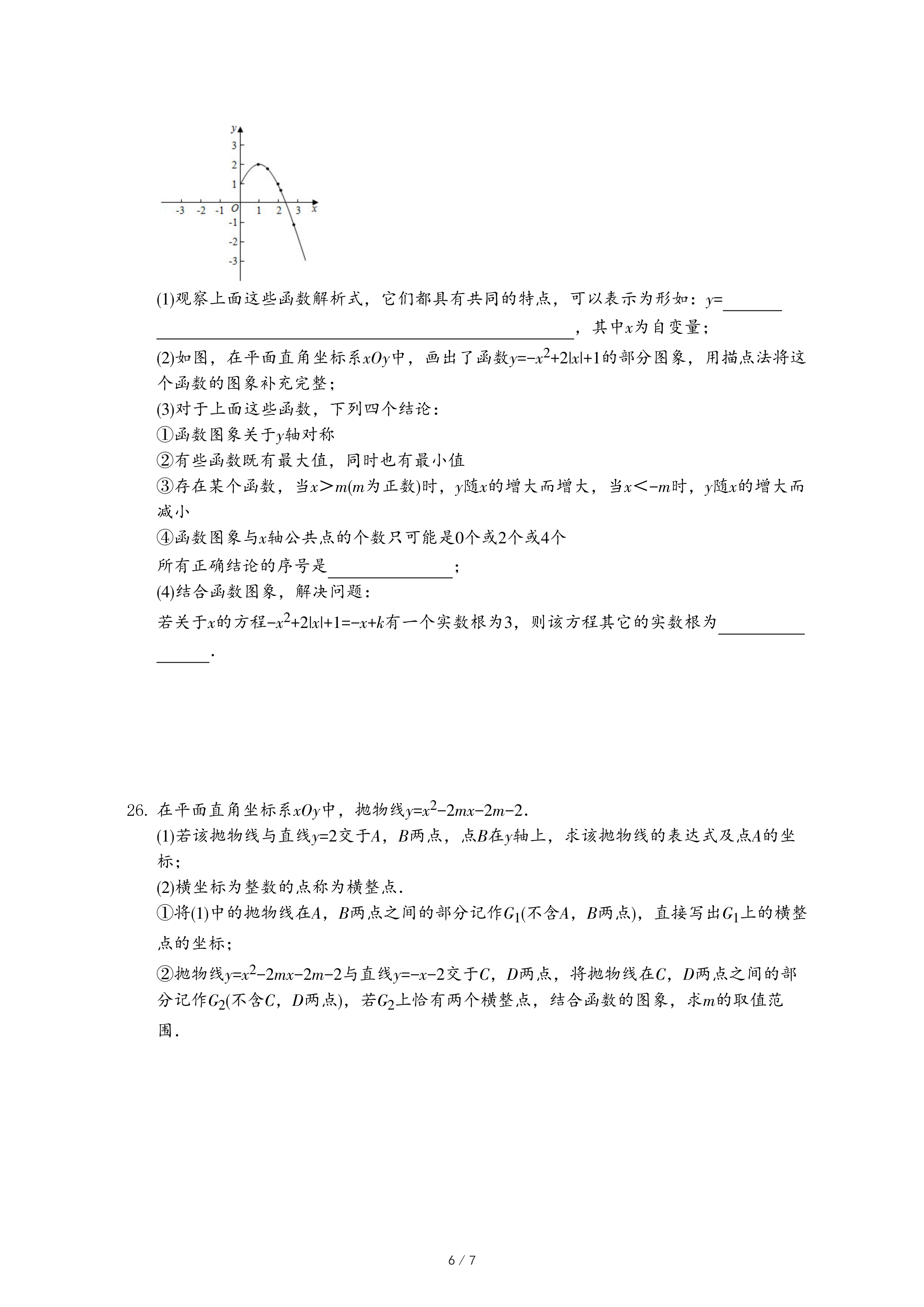
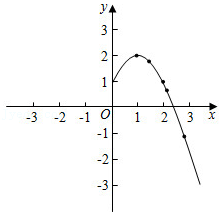25．下面给出六个函数解析式：
y=

1

2

x²，y=

√3

x²+1，y=-x²-

1

2

|x|，y=2x²-3|x|-1，y=-x²+2|x|+1，y=-3x²-|x|-4．
小明根据学习二次函数的经验，分析了上面这些函数解析式的特点，研究了它们的图象和性质．下面是小明的分析和研究过程，请补充完整：

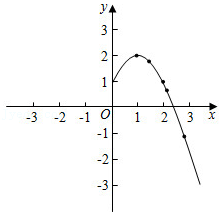
(1)观察上面这些函数解析式，它们都具有共同的特点，可以表示为形如：y=      ，其中x为自变量；
(2)如图，在平面直角坐标系xOy中，画出了函数y=-x²+2|x|+1的部分图象，用描点法将这个函数的图象补充完整；
(3)对于上面这些函数，下列四个结论：
①函数图象关于y轴对称
②有些函数既有最大值，同时也有最小值
③存在某个函数，当x＞m(m为正数)时，y随x的增大而增大，当x＜-m时，y随x的增大而减小
④函数图象与x轴公共点的个数只可能是0个或2个或4个
所有正确结论的序号是      ；
(4)结合函数图象，解决问题：
若关于x的方程-x²+2|x|+1=-x+k有一个实数根为3，则该方程其它的实数根为      ．

26．在平面直角坐标系xOy中，抛物线y=x²-2mx-2m-2．
(1)若该抛物线与直线y=2交于A，B两点，点B在y轴上，求该抛物线的表达式及点A的坐标；
(2)横坐标为整数的点称为横整点．
①将(1)中的抛物线在A，B两点之间的部分记作G₁(不含A，B两点)，直接写出G₁上的横整点的坐标；
②抛物线y=x²-2mx-2m-2与直线y=-x-2交于C，D两点，将抛物线在C，D两点之间的部分记作G₂(不含C，D两点)，若G₂上恰有两个横整点，结合函数的图象，求m的取值范围．

27．△ABC是等边三角形，点P在BC的延长线上，以P为中心，将线段PC逆时针旋转n°(0＜n＜180)得线段PQ，连接AP，BQ．
(1)如图1，若PC=AC，画出当BQ∥AP时的图形，并写出此时n的值；
(2)M为线段BQ的中点，连接PM．写出一个n的值，使得对于BC延长线上任意一点P，总有MP=

1

2

AP，并说明理由．

28．对于给定的△ABC，我们给出如下定义：
若点M是边BC上的一个定点，且以M为圆心的半圆上的所有点都在△ABC的内部或边上，则称这样的半圆为BC边上的点M关于△ABC的内半圆，并将半径最大的内半圆称为点M关于△ABC的最大内半圆．
若点M是边BC上的一个动点(M不与B，C重合)，则在所有的点M关于△ABC的最大内半圆中，将半径最大的内半圆称为BC关于△ABC的内半圆．

(1)在Rt△ABC中，∠BAC=90°，AB=AC=2，
①如图1，点D在边BC上，且CD=1，直接写出点D关于△ABC的最大内半圆的半径长；
②如图2，画出BC关于△ABC的内半圆，并直接写出它的半径长；
(2)在平面直角坐标系xOy中，点E的坐标为(3，0)，点P在直线y=

√3

3

x上运动(P不与O重合)，将OE关于△OEP的内半圆半径记为R，当

3

4

≤R≤1时，求点P的横坐标t的取值范围．