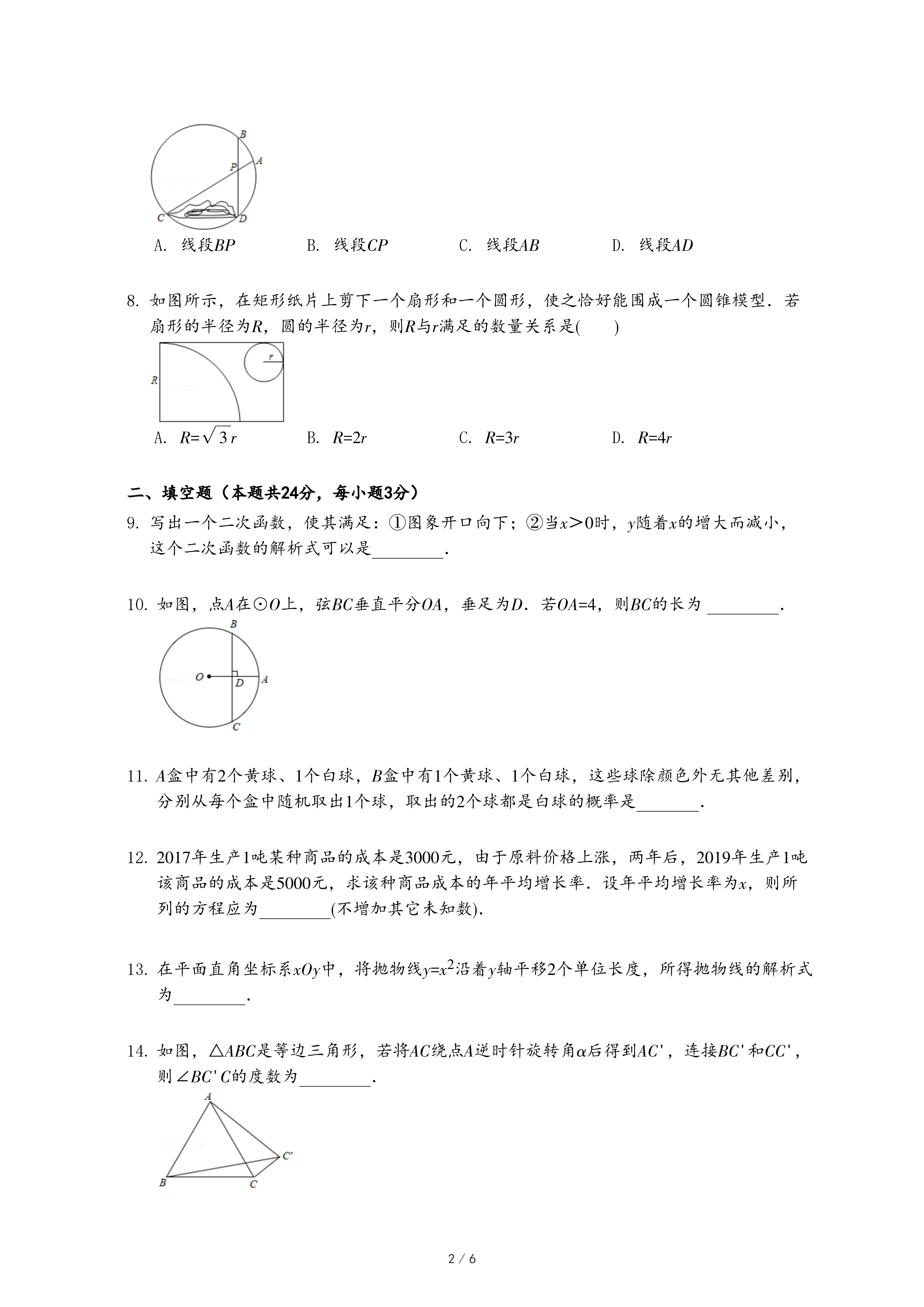
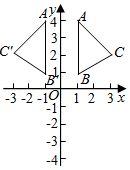
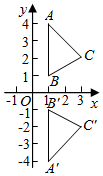
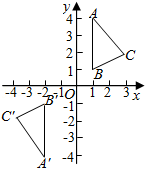
25.在平面直角坐标系xOy中,⊙O的半径为1.
给出如下定义:记线段AB的中点为M,当点M不在⊙O上时,平移线段AB,使点M落在⊙O上,得到线段A'B'(A',B'分别为点A,B的对应点)线段AA'长度的最小值称为线段AB到⊙O的“平移距离”.
(1)已知点A的坐标为(-1,0),点B在x轴上.若点B与原点O重合,则线段AB到⊙O的“平移距离”为
;
(2)若线段AB到⊙O的“平移距离”为2,则点B的坐标为
;
(3)若点A,B都在直线y=
x+4上,且AB=2,记线段AB到⊙O的“平移距离”为d
1,求d
1的最小值;
(4)若点A的坐标为(3,4),且AB=2,记线段AB到⊙O的“平移距离”为d
2,直接写出d
2的取值范围.