19．计算：
（1）3×；
（2）+÷．

20．如图，在中，点E，F分别在边AB，CD上，BE=DF，EF与对角线AC相交于点O．求证：OE=OF．

21．我国古代数学著作《九章算术》中有这样一个问题：今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适与岸齐．问水深、葭长各几何．(1丈=10尺）
大意是：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．水的深度与这根芦苇的长度分别是多少？
将这个实际问题转化为数学问题，根据题意画出图形（如图所示），其中水面宽AB=10尺，线段CD，CB表示芦苇，CD⊥AB于点E．
（1）图中DE=      尺，EB=      尺；
（2）求水的深度与这根芦苇的长度．

22．在∆ABC中，∠ACB=90°，点D是边AB上的一个动点，连接CD．作AE//DC，CE//AB，连接ED．
（1）如图1，当CD⊥AB时，求证：AC=ED；
（2）如图2，当D是AB的中点时，
①四边形ADCE的形状是       ；（填“矩形”、“菱形”或“正方形” )
②若AB=10，ED=8，则四边形ADCE的面积为       ．

23．对于函数y=|x-1|，小芸探究了该函数的部分性质，下面是小芸的探究过程，请补充完整：
（1）①对于函数y=|x-1|，当x≤1时，y=-x+1；当x>1时，y=      ；
②当x≤1时，函数y=|x-1|的图象如图所示，请在图中补全函数y=|x-1|的图象；
（2）当y=3时，x=      ；
（3）若点A（-1，y₁）和B（x₂，y₂）都在函数y=|x-1|的图象上，且y₂>y₁，结合函数图象，直接写出x₂的取值范围．

24．某校七年级和八年级学生人数都是200人，学校想了解这两个年级学生的阅读情况，分别从每个年级随机抽取了40名学生进行调查，收集了这80名学生一周阅读时长的数据，并对数据进行了整理、描述和分析．下面给出了部分信息．
a．七、八年级各抽取的40名学生一周阅读时长统计图（不完整）如图（两个年级的数据都分成6组：0≤x<2，2≤x<4，4≤x<6，6≤x<8，8≤x<10，10≤x<12)．
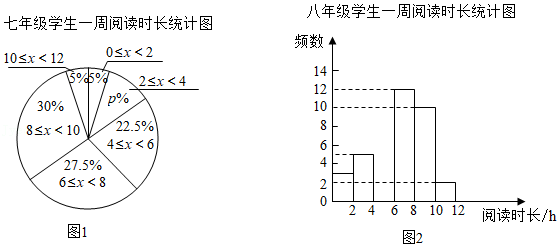
b．八年级学生一周阅读时长在6≤x<8这一组的数据是：6 6 6 6 6.5 6.5 7 7 7 7 7.5 7.5．
c．七、八年级学生一周阅读时长的平均数、中位数和众数如表：

根据以上信息，回答下列问题：
（1）图1中p%=      %；
（2）①补全八年级学生一周阅读时长统计图（图2)；
②上表中m的值为      ；
（3）将收集的这80名学生的数据分年级由大到小进行排序，其中有一名学生一周阅读时长是6.5小时，排在本年级的前20名，由此可以推断他是      年级的学生；（填“七”或“八” )
（4）估计两个年级共400名学生中，一周阅读时长不低于8小时的人数．

25．在平面直角坐标系xOy中，点A在x轴的正半轴上，点B在第一象限，作射线OB．给出如下定义：如果点P在∠BOA的内部过点P作PM⊥OA于点M，PN⊥OB于点N，那么称PM与PN的长度之和为点P关于∠BOA的“内距离”，记作d（P，∠BOA），即d（P，∠BOA）=PM+PN．
（1）如图1，若点P（3，2）在∠BOA的平分线上，则PM=      ，PN=      ，d（P，∠BOA）=      ；
（2）如图2，若∠BOA=75°，点C（a，a）（其中a>0）满足d（C，∠BOA）=2+，求a的值；
（3）若∠BOA=60°，点Q（m，n）在∠BOA的内部，用含m，n的式子表示d（Q，∠BOA），并直接写出结果．

26．已知∠MON=90°，点A是射线ON上的一个定点，点B是射线OM上的一个动点，且满足OB>OA．点C在线段OA的延长线上，且AC=OB．
（1）如图1，CD//OB，CD=OA，连接AD，BD；
①∆AOB与△      全等，∠OBA+∠ADC=      °；
②若OA=a，OB=b，则BD=      ；（用含a，b的式子表示）
（2）如图2，在线段BO上截取BE，使BE=OA，连接CE．若∠OBA+∠OCE=β，当点B在射线OM上运动时，β的大小是否会发生变化？如果不变，请求出这个定值；如果变化，请说明理由．

28．如图，∆ABC和∆DCE都是等边三角形，∠ACD=α(60°<α<120°)，点P，Q，M分别是AD，CD，CE的中点．
（1）求∠PQM的度数；（用含α的式子表示）
（2）若点N是BC的中点，连接NM，NP，PM，求证：∆PNM是等边三角形．

29．在平面直角坐标系xOy中，对于任意两点M（x₁，y₁），N（x₂，y₂），我们将|x₁-x₂|+2|y₁-y₂|称为点M与点N的“纵2倍直角距离”，记作d_MN．
例如：点M（-2，7）与N（5，6）的“纵2倍直角距离” d_MN=|-2-5|+2|7-6|=9．
（1）①已知点P₁（1，1），P₂（-4，0），P₃（0，），则在这三个点中，与原点O的“纵2倍直角距离”等于3的点是       、      ；
②已知点P（x，y），其中y≥0．若点P与原点O的“纵2倍直角距离” d_PO=3，请在下图中画出所有满足条件的点P组成的图形．
（2）若直线y=2x+b上恰好有两个点与原点O的“纵2倍直角距离”等于3，求b的取值范围；
（3）已知点A（1，1），B（3，1），点T（t，0）是x轴上的一个动点，正方形CDEF的顶点坐标分别为C（t-，0），D（t，），E（t+，0），F（t，-）．若线段AB上存在点G，正方形CDEF上存在点H，使得d_GH=5，直接写出t的取值范围．